题目内容
【题目】已知函数f(x)=|x﹣1|+|3x﹣ ![]() |.
|.
(1)求不等式f(x)<1的解集;
(2)若实数a,b,c满足a>0,b>0,c>0且a+b+c= ![]() .求证:
.求证: ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]() .
.
【答案】
(1)解:由f(x)<1,得|x﹣1|+|3x﹣ ![]() |<1可化为:
|<1可化为:
 或
或 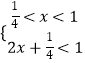 或
或  ,
,
得 ![]() <x<
<x< ![]() ,
,
所以f(x)<1的解集为:{x| ![]() <x<
<x< ![]() }
}
(2)解:因为a+b+c= ![]() ,
,
所以: ![]() +a+
+a+ ![]() +b+
+b+ ![]() +c≥2(a+b+c)=3,
+c≥2(a+b+c)=3,
所以: ![]() +
+ ![]() +
+ ![]() ≥
≥ ![]()
【解析】(1)通过讨论x的范围求出不等式的解集即可;(2)根据基本不等式的性质证明即可.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.

【题目】若定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() 是奇函数,现给出下列4个结论:①
是奇函数,现给出下列4个结论:①![]() 是周期为4的周期函数;
是周期为4的周期函数;
②![]() 的图象关于点
的图象关于点![]() 对称;
对称;
③![]() 是偶函数;
是偶函数;
④![]() 的图象经过点
的图象经过点![]() ,其中正确结论的序号是__________(请填上所有正确的序号).
,其中正确结论的序号是__________(请填上所有正确的序号).
【题目】某风景区水面游览中心计划国庆节当日投入之多3艘游船供游客观光,过去10年的数据资料显示每年国庆节当日客流量X(单位:万人)都大于1,并把客流量分成三段整理得下表:
国庆节当日客流量X | 1<X<3 | 3≤X≤5 | X>5 |
频数 | 2 | 4 | 4 |
以这10年的数据资料记录的隔断客流量的频率作为每年客流量在隔断发生的概率,且每年国庆节当日客流量相互独立.
(1)求未来连续3年国庆节当日中,恰好有1年国庆节当日客流量超过5万人的概率;
(2)该水面游览中心希望投入的游船尽可能使用,但每年国庆节当日游船最多使用量:(单位:艘)受当日客流量X(单位:万人)的限制,其关联关系如下表:
国庆节当日客流量X | 1<X<3 | 3≤X≤5 | X>5 |
游船最多使用量 | 1 | 2 | 3 |
若某艘游船国庆节当日使用,则水面游览中心国庆节当日可获得利润3万元,若某艘游船国庆节当日不使用,则水面游览中心国庆节当日亏损0.5万元,记Y(单位:万元)表示该水面游览中心国庆节当日获得总利润,当Y的数学期望最大时称水面游览中心在国庆节当日效益最佳,问该水面游览中心的国庆节当日应投入多少艘游船才能使该水面游览中心在国庆节当日效益最佳?



