题目内容
【题目】已知函数![]() .
.
(1)证明:函数![]() 在区间
在区间![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() ;
;
(2)证明:函数![]() 有且仅有两个零点.
有且仅有两个零点.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)求出![]() ,再说明
,再说明![]() 在区间
在区间![]() 单调递增,且
单调递增,且![]() ,
,![]() 即可。
即可。
(2)验证![]() ,即
,即![]() 是函数
是函数![]() 的一个零点;说明当
的一个零点;说明当![]() 无零点;当
无零点;当![]() 时有且仅有一个零点。即得证。
时有且仅有一个零点。即得证。
证明:(1)由![]() .
.
令![]() ,当
,当![]() 时,函数
时,函数![]() 为增函数,指数函数
为增函数,指数函数![]() 也为增函数,故当
也为增函数,故当![]() 时,函数
时,函数![]() 为增函数.
为增函数.
又因为![]() ,可得
,可得![]() ,有
,有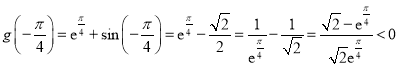 ,
,
![]() ,故存在唯一的
,故存在唯一的![]() 使得
使得![]() .
.
所以当![]() 时
时![]() ,即
,即![]() ;当
;当![]() 时,
时,![]() ,即
,即![]() ,所以函数
,所以函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,
上单调递增,
所以函数![]() 在区间
在区间![]() 存在唯一的极小值点
存在唯一的极小值点![]() ,且
,且![]() .
.
(2)①由![]() ,可得
,可得![]() 是函数
是函数![]() 的一个零点;
的一个零点;
②当![]() 时,
时,![]() ,
,![]() ,可得
,可得![]() ,此时函数
,此时函数![]() 没有零点;
没有零点;
③当![]() 时,由
时,由![]() .
.
由(1)知![]() ,可得函数
,可得函数![]() 在区间
在区间![]() 上有且仅有一个零点.
上有且仅有一个零点.
综上,函数![]() 有且仅有两个零点.
有且仅有两个零点.

【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如下表所示.
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 | 0.050 |
第2组 |
| n | 0.350 |
第3组 |
| 30 | p |
第4组 |
| 20 | 0.200 |
第5组 |
| 10 | 0.100 |
合计 | 100 | 1.000 |
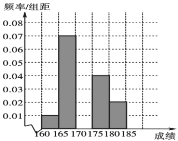
(1)求频率分布表中n,p
(2)为了能选拔出最优秀的学生,高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试,则第3、4、5组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定从6名学生中随机抽取2名学生接受甲考官的面试,求第4组至少有1名学生被甲考官面试的概率.
【题目】某企业通过调查问卷(满分50分)的形式对本企业900名员工的工作满意程度进行调查,并随机抽取了其中30名员工(16名女工,14名男工)的得分,如下表:
女 | 47 | 36 | 32 | 48 | 34 | 44 | 43 | 47 | 46 | 41 | 43 | 42 | 50 | 43 | 35 | 49 |
男 | 37 | 35 | 34 | 43 | 46 | 36 | 38 | 40 | 39 | 32 | 48 | 33 | 40 | 34 |
(1)根据以上数据,估计该企业得分大于45分的员工人数;
(2)现用计算器求得这30名员工的平均得分为40.5分,若规定大于平局得分为 “满意”,否则为 “不满意”,请完成下列表格:
“满意”的人数 | “不满意”的人数 | 合计 | |
女员工 | 16 | ||
男员工 | 14 | ||
合计 | 30 |
(3)根据上述表中数据,利用独立性检验的方法判断,能否在犯错误的概率不超过1%的前提下,认为该企业员工“性别”与“工作是否满意”有关?
参考数据:
P(K2 | 0.10 | 0.050 | 0.025 | 0.010 | 0.001 |
K | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
![]()