题目内容
【题目】某IT从业者绘制了他在26岁~35岁(2009年~2018年)之间各年的月平均收入(单位:千元)的散点图:

(1)由散点图知,可用回归模型![]() 拟合
拟合![]() 与
与![]() 的关系,试根据附注提供的有关数据建立
的关系,试根据附注提供的有关数据建立![]() 关于
关于![]() 的回归方程
的回归方程
(2)若把月收入不低于2万元称为“高收入者”.

试利用(1)的结果,估计他36岁时能否称为“高收入者”?能否有95%的把握认为年龄与收入有关系?
附注:①.参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中
,其中![]() ,取
,取![]() ,
,![]()
②.参考公式:回归方程![]() 中斜率
中斜率![]() 和截距
和截距![]() 的最小二乘估计分别为:
的最小二乘估计分别为: ,
,![]()
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
③. .
.

【答案】(1)![]() (2)他36岁时能称为“高收入者”,有95%的把握认为年龄与收入有关系
(2)他36岁时能称为“高收入者”,有95%的把握认为年龄与收入有关系
【解析】
(1)分别计算出![]() ,
,![]() ,带入即可。
,带入即可。
(2)将2代入比较即可,计算观测值,与临界值比较可得结论。
(1)令![]() ,则
,则![]()
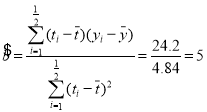
![]()
∴![]()
∴![]()
(2)把![]() 带入
带入![]()
![]() (千元)≥2(万元)
(千元)≥2(万元)
∴他36岁时能称为“高收入者”.
![]()
故有95%的把握认为年龄与收入有关系

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】支付宝作为一款移动支付工具,在日常生活中起到了重要的作用.巴蜀中学高2018届学生为了调查支付宝在人群中的使用情况,在街头随机对![]() 名市民进行了调查,结果如下.
名市民进行了调查,结果如下.
(1)对![]() 名市民按年龄以及是否使用支付宝进行分组,得到以下表格,试问能否有
名市民按年龄以及是否使用支付宝进行分组,得到以下表格,试问能否有![]() 的把握认为“使用支付宝与年龄有关”?
的把握认为“使用支付宝与年龄有关”?
使用支付宝 | 不使用支付宝 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(2)现采用分层抽样的方法,从被调查的![]() 岁以下的市民中抽取了
岁以下的市民中抽取了![]() 位进行进一步调查,然后从这
位进行进一步调查,然后从这![]() 位市民中随机抽取
位市民中随机抽取![]() 位,求至少抽到
位,求至少抽到![]() 位“使用支付宝”的市民的概率;
位“使用支付宝”的市民的概率;
(3) 为了鼓励市民使用支付宝,支付宝推出了“奖励金”活动,每使用支付宝支付一次,分别有![]() 的概率获得
的概率获得![]() 元奖励金,每次支付获得的奖励金情况互不影响.若某位市民在一周使用了
元奖励金,每次支付获得的奖励金情况互不影响.若某位市民在一周使用了![]() 次支付宝,记
次支付宝,记![]() 为这一周他获得的奖励金数,求
为这一周他获得的奖励金数,求![]() 的分布列和数学期望.
的分布列和数学期望.
附:![]() ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】为调查人们在购物时的支付习惯,某超市对随机抽取的600名顾客的支付方式进行了统计,数据如下表所示:
支付方式 | 微信 | 支付宝 | 购物卡 | 现金 |
人数 | 200 | 150 | 150 | 100 |
现有甲、乙、丙三人将进入该超市购物,各人支付方式相互独立,假设以频率近似代替概率.
(1)求三人中使用微信支付的人数多于现金支付人数的概率;
(2)记![]() 为三人中使用支付宝支付的人数,求
为三人中使用支付宝支付的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
