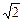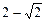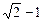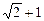题目内容

(1)∵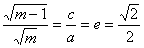 ∴m=2 (2)如图,MN和PQ是椭圆
∴m=2 (2)如图,MN和PQ是椭圆 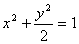 的两条弦,相交于焦点
的两条弦,相交于焦点
F(0,1),且PQ⊥MN,直线PQ和MN中至少有一条存在斜率,
不妨设PQ的斜率为k,PQ的方程为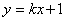 代入椭圆方程得:
代入椭圆方程得: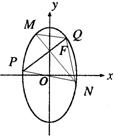
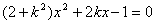
设P、Q两点的坐标分别为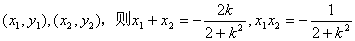
从而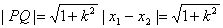 ·
·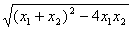
亦即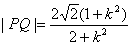 ①当
①当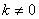 时,MN的斜率为
时,MN的斜率为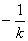 ,同上可推得
,同上可推得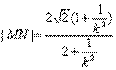 ,故四边形面积
,故四边形面积
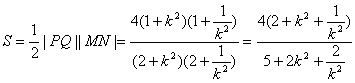
令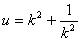 得
得 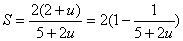 ∵
∵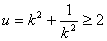
当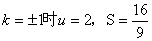 且S是以u为自变量的增函数
且S是以u为自变量的增函数
∴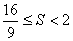 ②当k=0时,MN为椭圆长轴,|MN|=
②当k=0时,MN为椭圆长轴,|MN|=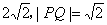
∴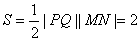 综合①②
综合①② 知四边形PMQN的最大值为2,最小值为
知四边形PMQN的最大值为2,最小值为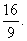
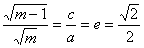 ∴m=2 (2)如图,MN和PQ是椭圆
∴m=2 (2)如图,MN和PQ是椭圆 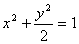 的两条弦,相交于焦点
的两条弦,相交于焦点F(0,1),且PQ⊥MN,直线PQ和MN中至少有一条存在斜率,
不妨设PQ的斜率为k,PQ的方程为
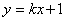 代入椭圆方程得:
代入椭圆方程得:
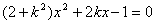
设P、Q两点的坐标分别为
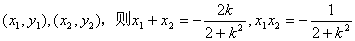
从而
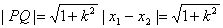 ·
·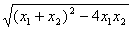
亦即
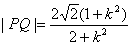 ①当
①当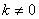 时,MN的斜率为
时,MN的斜率为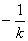 ,同上可推得
,同上可推得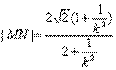 ,故四边形面积
,故四边形面积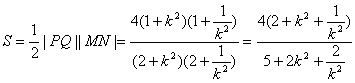
令
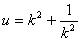 得
得 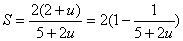 ∵
∵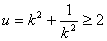
当
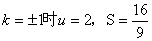 且S是以u为自变量的增函数
且S是以u为自变量的增函数∴
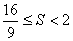 ②当k=0时,MN为椭圆长轴,|MN|=
②当k=0时,MN为椭圆长轴,|MN|=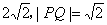
∴
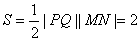 综合①②
综合①② 知四边形PMQN的最大值为2,最小值为
知四边形PMQN的最大值为2,最小值为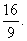
略

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
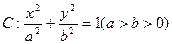 的离心率是
的离心率是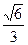 ,长轴长是为6,
,长轴长是为6,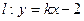 与
与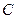 交于
交于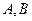 两点,已知点
两点,已知点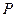 的坐标为
的坐标为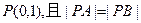 ,求直线
,求直线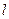 的方程。
的方程。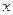 轴上,椭圆上的点到左、右焦点
轴上,椭圆上的点到左、右焦点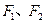 的距离之和为
的距离之和为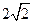 ,离心率
,离心率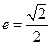 .
. 的直线
的直线 与椭圆C交于点
与椭圆C交于点 ,以
,以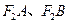 为邻边作平行四边形
为邻边作平行四边形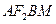 ,求该平行四边形对角线
,求该平行四边形对角线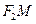 的长度的取值范围.
的长度的取值范围.
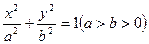 的左、右焦点分别为
的左、右焦点分别为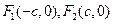 ,若椭圆上存在一点
,若椭圆上存在一点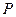 (非顶点)使
(非顶点)使
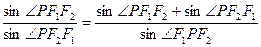 ,则该椭圆的离心率的取值范围是 .
,则该椭圆的离心率的取值范围是 .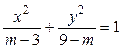 表示椭圆,则m的取值范围是_____________
表示椭圆,则m的取值范围是_____________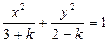 表示椭圆,则
表示椭圆,则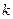 的实数取值范围为
的实数取值范围为 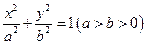 的四个顶点为A、B、C、D,若四边形ABCD的内切圆恰好过焦点,则椭圆的离心率为( )
的四个顶点为A、B、C、D,若四边形ABCD的内切圆恰好过焦点,则椭圆的离心率为( )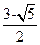 B.
B.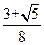 C.
C.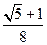 D.
D.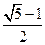
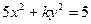 的一个焦点是
的一个焦点是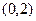 ,那
,那 么
么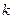 等于( )
等于( )
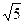 D
D 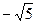
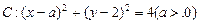 及直线l:x-y+3=O,当直线l被圆C截得的
及直线l:x-y+3=O,当直线l被圆C截得的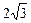 时,则a=( )
时,则a=( )