题目内容
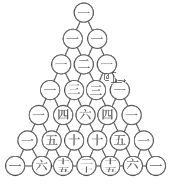
【题目】杨辉三角，又称帕斯卡三角，是二项式系数在三角形中的一种几何排列.在我国南宋数学家杨辉所著的《详解九章算法》（1261年）一书中用如图所示的三角形解释二项式乘方展开式的系数规律.现把杨辉三角中的数从上到下，从左到右依次排列，得数列：1,1,1,1,2,1,1,3,3,1,1,4,6,4,1…….记作数列
，若数列的前
项和为
，则
（ ）
A. 
B. 
C. 
D. 
【答案】B
【解析】
数列{an}中前78项在杨辉三角的从第一排到第12排，每排的和为二项式系数和, {an}中最后两项是第13排的1和12．全部相加可得结果.
杨辉三角中前12行共有1+2+3+4+…+12＝78个数，其和为：20+21+22+…+211＝212﹣1＝4095；
第13行共有2个位数，它们是1，12，其和为13，
故
＝4095+13＝4108，
故选：B．
练习册系列答案
相关题目
【题目】在万众创新的大经济背景下，某成都青年面包店推出一款新面包，每个面包的成本价为
元，售价为
元，该款面包当天只出一炉（一炉至少
个，至多
个），当天如果没有售完，剩余的面包以每个
元的价格处理掉，为了确定这一炉面包的个数，该店记录了这款新面包最近天的日需求量（单位：个），整理得下表：
日需求量 |
|
|
|
|
|
频数 |
|
|
|
|
|
（1）根据表中数据可知，频数
与日需求量
（单位：个）线性相关，求关于
的线性回归方程；
（2）以天记录的各日需求量的频率代替各日需求量的概率，若该店这款新面包出炉的个数为
，记当日这款新面包获得的总利润为
（单位：元）.求的分布列及其数学期望.
相关公式：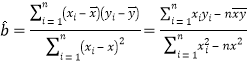
，
