题目内容
10．已知函数f（x）=$\left\{\begin{array}{l}{1-|1-x|，x∈（-∞，2）}\\{2f（x-2），x∈[2，+∞）}\end{array}\right.$，设方程f（x）=2${\;}^{\frac{x-1}{2}}$的根从小到大依次为x1，x2，…xn，…，n∈N*，则数列{f（xn）}的前n项和为（ ）| A． | n2 | B． | n2+n | C． | 2n-1 | D． | 2n+1-1 |
分析 作出函数f（x）=$\left\{\begin{array}{l}{1-|1-x|，x∈（-∞，2）}\\{2f（x-2），x∈[2，+∞）}\end{array}\right.$的图象，可得数列{f（xn）}从小到大依次为1，2，4，…，组成以1为首项，2为公比的等比数列，即可求出数列{f（xn）}的前n项和．
解答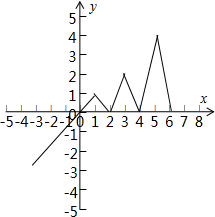 
解：函数f（x）=$\left\{\begin{array}{l}{1-|1-x|，x∈（-∞，2）}\\{2f（x-2），x∈[2，+∞）}\end{array}\right.$的图象如图所示，
x=1时，f（x）=1，x=3时，f（x）=2，x=5时，f（x）=4，
所以方程f（x）=2${\;}^{\frac{x-1}{2}}$的根从小到大依次为1，3，5，…，数列{f（xn）}从小到大依次为1，2，4，…，组成以1为首项，2为公比的等比数列，
所以数列{f（xn）}的前n项和为$\frac{1-{2}^{n}}{1-2}$=2n-1，
故选：C．
点评 本题考查方程根，考查数列的求和，考查学生分析解决问题的能力，正确作图，确定数列{f（xn）}从小到大依次为1，2，4，…，组成以1为首项，2为公比的等比数列是关键．
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
如图在以OA为半径的半圆M中，有三个半径为1的相同的半圆，在半圆M中任取一点N．