题目内容
【题目】在数列{an}中，a1＝2，an＋1＝4an－3n＋1，n∈N*.
(1)求证：数列{an－n}是等比数列；
(2)求数列{an}的前n项和Sn；
(3)求证：不等式Sn＋1≤4Sn对任意n∈N*皆成立．
【答案】（1）见解析（2）
（3）见解析
【解析】(1)证明：由题设an＋1＝4an－3n＋1，得an＋1－(n＋1)＝4(an－n)，n∈N*.又a1－1＝1，所以数列{an－n}是首项为1，公比为4的等比数列．
(2)解：由(1)可知an－n＝4n－1，于是数列{an}的通项公式为an＝4n－1＋n，所以数列{an}的前n项和Sn＝.
(3)证明：对任意的n∈N*，Sn＋1－4Sn＝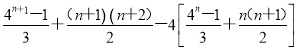
＝－
(3n2＋n－4)≤0，所以不等式Sn＋1≤4Sn对任意n∈N*皆成立．
练习册系列答案
相关题目
【题目】某地区甲校高二年级有1 100人，乙校高二年级有900人，为了统计两个学校高二年级在学业水平考试中的数学学科成绩，采用分层抽样的方法在两校共抽取了200名学生的数学成绩，如下表：（已知本次测试合格线是50分，两校合格率均为100%）
甲校高二年级数学成绩：
分组 | [50,60） | [60,70） | [70,80） | [80,90） | [90,100] |
频数 | 10 | 25 | 35 | 30 | x |
乙校高二年级数学成绩：
分组 | [50,60） | [60,70） | [70,80） | [80,90） | [90,100] |
频数 | 15 | 30 | 25 | y | 5 |
（1）计算x，y的值，并分别估计以上两所学校数学成绩的平均分（精确到1分）．
（2）若数学成绩不低于80分为优秀，低于80分的为非优秀，根据以上统计数据写下面2×2列联表，并回答能否在犯错误的概率不超过0．05的前提下认为“两个学校的数学成绩有差异？”
甲校 | 乙校 | 总计 | |
优秀 | |||
非优秀 | |||
总计 |
