题目内容
【题目】已知空间三点![]() ,
,![]() ,
,![]()
(1)求以![]() 为边的平行四边形的面积;
为边的平行四边形的面积;
(2)若向量a分别与![]() 垂直,且|a|=
垂直,且|a|=![]() ,求a的坐标.
,求a的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)由已知中空间三点![]() ,我们分别求出向量
,我们分别求出向量![]() 的坐标,根据模相等及夹角,判断出三角形
的坐标,根据模相等及夹角,判断出三角形![]() 为等边三角形,从而得到以向量
为等边三角形,从而得到以向量![]() 为一组邻边的平行四边形的面积
为一组邻边的平行四边形的面积![]() ;(2)根据(1)中结论,易知向量
;(2)根据(1)中结论,易知向量![]() 分别与向量
分别与向量![]() 垂直,且
垂直,且![]() ,设出向量
,设出向量![]() 的坐标,进而构造方程组,解方程组即可求出向量
的坐标,进而构造方程组,解方程组即可求出向量![]() 的坐标.
的坐标.
(1)∵![]() =(-2,-1,3),
=(-2,-1,3),![]() =(1,-3,2),
=(1,-3,2),
∴|![]() |=
|=![]() ,|
,|![]() |=
|=![]() ,cos∠BAC=
,cos∠BAC=![]() =,∴∠BAC=60°,
=,∴∠BAC=60°,
∴S=|![]() |·|
|·|![]() |sin∠BAC=7
|sin∠BAC=7![]() .
.
(2)设向量a=(x,y,z),则由a·![]() =0,a·
=0,a·![]() =0,|a|=
=0,|a|=![]() ,得
,得
 ∴
∴![]() 或
或![]()
∴a=(1,1,1)或(-1,-1,-1).

练习册系列答案
相关题目
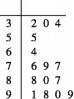
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|