题目内容
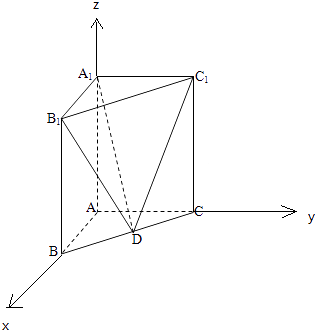
【题目】如图,在直三棱柱ABC﹣A1B1C1中,已知AB⊥AC,AB=2,AC=4,AA1=3.D是线段BC的中点. 
(1)求直线DB1与平面A1C1D所成角的正弦值;
(2)求二面角B1﹣A1D﹣C1的大小的余弦值.
【答案】
(1)解:因为在直三棱柱ABC﹣A1B1C1中,AB⊥AC,
所以分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,
则A(0,0,0),B(2,0,0),C(0,4,0),A1(0,0,3),B1(2,0,3),C1(0,4,3),
因为D是BC的中点,所以D(1,2,0),
因为 ![]() ,设平面A1C1D的法向量
,设平面A1C1D的法向量 ![]() ,
,
则 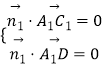 ,即
,即 ![]() ,取
,取 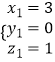 ,
,
所以平面A1C1D的法向量 ![]() ,而
,而 ![]() ,
,
所以 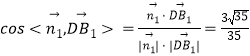 ,
,
所以直线DB1与平面A1C1D所成角的正弦值为 ![]()
(2)解: ![]() ,
, ![]() ,
,
设平面B1A1D的法向量 ![]() ,
,
则 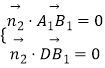 ,即
,即 ![]() ,
,
取  ,平面B1A1D的法向量
,平面B1A1D的法向量 ![]() ,
,
所以 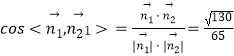 ,
,
二面角B1﹣A1D﹣C1的大小的余弦值 ![]() .
.
【解析】(1)分别以AB、AC、AA1所在的直线为x轴、y轴、z轴,建立空间直角坐标系,利用向量法能求出直线DB1与平面A1C1D所成角的正弦值.(2)求出平面B1A1D的法向量和平面B1A1D的法向量,利用向量法能求出二面角B1﹣A1D﹣C1的大小的余弦值.
【考点精析】根据题目的已知条件,利用空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则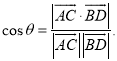 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|
