题目内容
设定义域为R的函数f(x)=
且关于x的方程f2(x)+bf(x)+c=0有7个不同实数解,令m=2010b,n=2010c,则( )
|
分析:画出函数的图象,通过方程f2(x)+bf(x)+c=0有7个不同实数解,求出a,b的值,即可判断m,n的大小.
解答: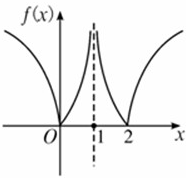 解:函数f(x)=
解:函数f(x)=
的图象,如图.
由图知,f(x)图象关于x=1对称,且f(x)≥0,
若方程f2(x)+bf(x)+c=0 ①有7个解,
则方程t2+bt+c=0 ②有两个不等实根,且一根为正,一根为0.否则,
若方程②有两相等实根,则方程①至多有4个解,
若方程②有两个不等正实根,则方程①有8个解.
∵f(x)=0满足方程,则c=0,
又∵另一个f(x)>0,
∴b=-f(x)<0.
故b<0且c=0,
m=2010b∈(0,1),n=2010c=1;
所以m<n.
故选A.
 解:函数f(x)=
解:函数f(x)=
|
由图知,f(x)图象关于x=1对称,且f(x)≥0,
若方程f2(x)+bf(x)+c=0 ①有7个解,
则方程t2+bt+c=0 ②有两个不等实根,且一根为正,一根为0.否则,
若方程②有两相等实根,则方程①至多有4个解,
若方程②有两个不等正实根,则方程①有8个解.
∵f(x)=0满足方程,则c=0,
又∵另一个f(x)>0,
∴b=-f(x)<0.
故b<0且c=0,
m=2010b∈(0,1),n=2010c=1;
所以m<n.
故选A.
点评:本题考查函数的图象,函数的零点与方程根的问题,考查数形结合,分类讨论思想,考查计算能力.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目