题目内容
已知数列 是各项均不为0的等差数列,公差为
是各项均不为0的等差数列,公差为 ,
, 为其前n项和,且满足
为其前n项和,且满足 ,
, .数列
.数列 满足
满足 ,
, ,
,  为数列
为数列 的前
的前 项和.
项和.
(1)求数列 的通项公式
的通项公式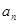 ;
;
(2)若对任意的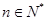 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(3)是否存在正整数 ,使得
,使得 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有
的值;若不存在,请说明理由.
(1)  ;(2)
;(2) ;(3)存在,
;(3)存在, ,
, .
.
解析试题分析:(1)利用通项公式和求和公式展开解析式,解方程组,得出 ,
, ,写出解析式;(2)先用裂项相消法求出
,写出解析式;(2)先用裂项相消法求出 ,再讨论
,再讨论 的奇数偶数两种情况,利用恒成立解题;(3)先利用等比中项列出表达式,解出
的奇数偶数两种情况,利用恒成立解题;(3)先利用等比中项列出表达式,解出 .
.
试题解析:(1)在 中,令
中,令 ,
,
得 即
即 2分
2分
解得 ,
, ,∴
,∴ 3分
3分
又∵ 时,
时, 满足
满足 ,∴
,∴ 4分
4分
(2)∵ , 5分
, 5分
∴ . 6分
. 6分
①当 为偶数时,要使不等式
为偶数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立. 7分
恒成立. 7分
∵ ,等号在
,等号在 时取得.
时取得. 此时
此时 需满足
需满足 . 8分
. 8分
②当 为奇数时,要使不等式
为奇数时,要使不等式 恒成立,即需不等式
恒成立,即需不等式 恒成立.
恒成立.
∴ 是随
是随 的增大而增大, ∴
的增大而增大, ∴ 时
时 取得最小值
取得最小值 .
.
此时 需满足
需满足 . 9分
. 9分
∴综合①、②可得 的取值范围是
的取值范围是 . 10分
. 10分
(3) ,
, ,
, ,
,
若 成等比数列,则
成等比数列,则 , 11分
, 11分
即 .
.
由 ,可得
,可得 , 12分
, 12分
即 ,
,
∴ . 13分
. 13分
又 ,且
,且 ,所以
,所以 ,此时
,此时 .
.
因此,当且仅当 ,
, 时,数列
时,数列 中的
中的 成等比数列. 14分
成等比数列. 14分
考点:1.等差数列的通项公式和求和公式;2.裂项相消法求和;3.等比中项.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
 的公比为q,且
的公比为q,且 ,
, 表示不超过实数
表示不超过实数 的最大整数(如
的最大整数(如 ),记
),记 ,数列
,数列 项和为
项和为 ,数列
,数列 的前
的前 .
. ,求
,求 ;
; (
( )的充分必要条件为
)的充分必要条件为 ;
; 的正整数n,都有
的正整数n,都有 ,证明:
,证明: .
. 中,
中, ,设
,设 .
. 的前三项;
的前三项; ;
; 项和为
项和为 ,求证:
,求证: .
. 的首项
的首项 ,公比
,公比 ,设数列
,设数列 的通项公式
的通项公式 ,数列
,数列 项和分别记为
项和分别记为 ,
, ,试比较
,试比较

 的通项公式;
的通项公式; 求数列
求数列 的前
的前 项和
项和 。
。 中,
中, ,
, .
. 满足
满足 ,数列
,数列 项和为
项和为 ,若不等式
,若不等式 对一切
对一切 恒成立,求
恒成立,求 的取值范围.
的取值范围. 的各项均为正数,
的各项均为正数, ,
, .
. .证明:
.证明: 为等差数列,并求
为等差数列,并求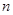 项和
项和 .
. 的前
的前 项和为
项和为 ,且
,且 .
. ;(Ⅱ)设
;(Ⅱ)设 ,求数列
,求数列 的通项公式。
的通项公式。 满足:
满足: (
( ).
). 的值;
的值; 是等比数列;
是等比数列; ,
, ,如果对任意
,如果对任意 ,都有
,都有 ,
, 的取值范围.
的取值范围.