题目内容
9．设全集U={1，2，3，4，5，6}，用U的子集可表示由0，1组成的6位字符串，如{2，4}； 表示的是笫2个字符为1，第4个字符为1，其余均为0的6位字符串010100，并规定空集表示的字符串为000000．①若M={2，3.6}，则∁UM表示的6位字符串为100110；
②若A={1，3}，集合A∪B表示的字符串为101001，则满足条件的集合B的个数是4．
分析 ①先求出M表示的6位字符串，从而求出∁UM表示的6位字符串；②由A={1，3}，集合A∪B表示的字符串为101001，求出集合B，从而得到答案．
解答 解：①M表示的6位字符串是：011001，
则∁UM表示的6位字符串为：100110；
②若A={1，3}，集合A∪B表示的字符串为101001，
∴集合B可能是{6}，{1，6}，{3，6}，{1，3，6}，
故答案为：100110，4．
点评 本题考察了集合的运算，考察新定义问题，是一道基础题．
练习册系列答案
新课标阶梯阅读训练系列答案
相关题目
如图，曲线C1：$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{4}$=1（y≤0）；曲线C2：x2=4y，自曲线C1上一点A作C2的两条切线，切点分别为B，C．
2．某高中有高一新生500名，分成水平相同的A，B两类进行教学实验．为对比教学效果，现用分层抽样的方法从A、B两类学生中分别抽取了40人、60人进行测试．
（Ⅰ）求该学校高一新生A、B两类学生各多少人？
（Ⅱ）经过测试，得到以下三个数据图表：
图一：75分以上A、B两类参加测试学生成绩的茎叶图（茎、叶分别是十位和个位上的数字）（如图1）
图二：100名测试学生成绩的频率分布直方图2；
表一：100名测试学生成绩频率分布表；
①先填写频率分布表（表一）中的六个空格，然后将频率分布直方图（图二）补充完整；
②该学校拟定从参加考试的79分以上（含79分）的B类学生中随机抽取2人代表学校参加市比赛，求抽到的2人分数都在80分以上的概率．
（Ⅰ）求该学校高一新生A、B两类学生各多少人？
（Ⅱ）经过测试，得到以下三个数据图表：
图一：75分以上A、B两类参加测试学生成绩的茎叶图（茎、叶分别是十位和个位上的数字）（如图1）
图二：100名测试学生成绩的频率分布直方图2；
表一：100名测试学生成绩频率分布表；
| 组号 | 分组 | 频数 | 频率 |
| 1 | [55，60） | 5 | 0.05 |
| 2 | [60，65） | 20 | 0.20 |
| 3 | [65，70） | ||
| 4 | [70，75） | 35 | 0.35 |
| 5 | [75，80） | ||
| 6 | [80，85） | ||
| 合计 | 100 | 1.00 | |
②该学校拟定从参加考试的79分以上（含79分）的B类学生中随机抽取2人代表学校参加市比赛，求抽到的2人分数都在80分以上的概率．
19．已知某几何体的三视图（单位：cm），如图所示，则此几何体的外接球的体积为（ ）
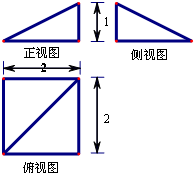
| A． | $\frac{9}{2}$πcm3 | B． | 36πcm3 | C． | $\frac{64}{3}$πcm3 | D． | 9πcm3 |