题目内容
已知函数f(x)=x2+alnx.
(I)当a=-2时,求函数f(x)的极值;
(II)若g(x)=f(x)+
在[1,+∞)上是单调增函数,求实数a的取值范围.
(I)当a=-2时,求函数f(x)的极值;
(II)若g(x)=f(x)+
| 2 |
| x |
(I)函数f(x)的定义域为(0,+∞)
当a=-2时,f′(x)=2x-
=
当x变化时,f′(x),f(x)的值变化情况如下表
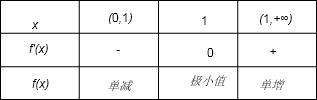
由上表可知,函数f(x)单调递减区间是(0,1),单调递增区间是(1,+∞)
极小值是f(1)=1,没有极大值
(2)由g(x)=x2+alnx+
得g′(x)=2x+
-
因为g(x)在[1,+∞)上是单调增函数
所以g′(x)≥0在[1,+∞)上恒成立
即不等式2x+
-
≥0在[1,+∞)上恒成立即a≥
-2x2在[1,+∞)上恒成立
令∅(x)=
-2x2则∅′(x)=-
-4x当x∈[1,+∞)时,∅′(x)=-
-4x<0
∴∅(x)=
-2x2在[1,+∞)上为减函数
∅(x)的最大值为∅(1)=0
∴a≥0
故a的取值范围为[0,+∞)
当a=-2时,f′(x)=2x-
| 2 |
| x |
| 2(x+1)(x-1) |
| x |
当x变化时,f′(x),f(x)的值变化情况如下表

由上表可知,函数f(x)单调递减区间是(0,1),单调递增区间是(1,+∞)
极小值是f(1)=1,没有极大值
(2)由g(x)=x2+alnx+
| 2 |
| x |
| a |
| x |
| 2 |
| x2 |
因为g(x)在[1,+∞)上是单调增函数
所以g′(x)≥0在[1,+∞)上恒成立
即不等式2x+
| a |
| x |
| 2 |
| x2 |
| 2 |
| x |
令∅(x)=
| 2 |
| x |
| 2 |
| x2 |
| 2 |
| x2 |
∴∅(x)=
| 2 |
| x |
∅(x)的最大值为∅(1)=0
∴a≥0
故a的取值范围为[0,+∞)

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目