题目内容
【题目】假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:
i | 1 | 2 | 3 | 4 | 5 |
|
xi | 2 | 3 | 4 | 5 | 6 | |
yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 | |
xi yi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 |
若由资料知,y对x呈线性相关关系,试求:
(1)回归直线方程;
(2)估计使用年限为10年时,维修费用约是多少
【答案】(1)![]() =1.23 x+0.08(2)12.38万元
=1.23 x+0.08(2)12.38万元
【解析】
(1)根据所给的数据,做出变量![]() ,
,![]() 的平均数,根据最小二乘法做出线性回归方程的系数
的平均数,根据最小二乘法做出线性回归方程的系数![]() ,在根据样本中心点一定在线性回归方程上,求出
,在根据样本中心点一定在线性回归方程上,求出![]() 的值,从而得到线性回归方程;(2)当自变量为10时,代入线性回归方程,求出当年的维修费用,这是一个预报值.
的值,从而得到线性回归方程;(2)当自变量为10时,代入线性回归方程,求出当年的维修费用,这是一个预报值.
(1)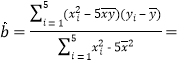
![]() =
=![]() =1.23.
=1.23.
![]() =5-1.23×4=0.08.
=5-1.23×4=0.08.![]() 回归直线方程为
回归直线方程为![]() =1.23 x+0.08.
=1.23 x+0.08.
(2)当![]() 时,
时,![]() =1.23×10+0.08=12.38万元,即估计用10年时,维修费约为12.38万元.
=1.23×10+0.08=12.38万元,即估计用10年时,维修费约为12.38万元.

【题目】某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验,得到的数据如下:
零件的个数 | 2 | 3 | 4 | 5 |
加工的时间 | 2.5 | 3 | 4 | 4.5 |
(Ⅰ)在给定的坐标系中画出表中数据的散点图;

(Ⅱ)试对![]() 与
与![]() 的关系进行相关性检验,如
的关系进行相关性检验,如![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(Ⅲ)试预测加工![]() 个零件需要多少时间?
个零件需要多少时间?
参考数据:![]() ,
,![]() .
.
附: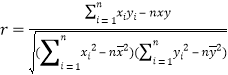 );
); ,
, ![]() ;
;
相关性检验的临界值表
n-2 | 小概率 | n-2 | 小概率 | n-2 | 小概率 | |||
0.05 | 0.01 | 0.05 | 0.01 | 0.05 | 0.01 | |||
1 | 0.997 | 1 | 4 | 0.811 | 0.917 | 7 | 0.666 | 0.798 |
2 | 0.950 | 0.990 | 5 | 0.754 | 0.874 | 8 | 0.632 | 0.765 |
3 | 0.878 | 0.959 | 6 | 0.707 | 0.834 | 9 | 0.602 | 0.735 |
注:表中的n为数据的组数
【题目】某班主任对全班50名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
分类 | 积极参加 班级工作 | 不太主动参 加班级工作 | 总计 |
学习积极性高 | 18 | 7 | 25 |
学习积极性一般 | 6 | 19 | 25 |
总计 | 24 | 26 | 50 |
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关,并说明理由.