Question

【题目】已知f（x）是定义在R上且以4为周期的奇函数，当x∈（0，2）时，f（x）=ln（x2﹣x+b），若函数f（x）在区间[﹣2，2]上的零点个数为5，则实数b的取值范围是

Answer 1

【答案】或b=
【解析】∵f（x）是定义在R上的奇函数，
故f（0）=0，即0是函数f（x）的零点，
又由f（x）是定义在R上且以4为周期的周期函数，
故f（﹣2）=f（2），且f（﹣2）=﹣f（2），
故f（﹣2）=f（2）=0，
即±2也是函数f（x）的零点，
若函数f（x）在区间[﹣2，2]上的零点个数为5，
则当x∈（0，2）时，f（x）=ln（x2﹣x+b），
故当x∈（0，2）时，x2﹣x+b＞0恒成立，
且x2﹣x+b=1在（0，2）有一解，
即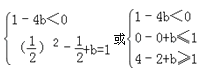
解得：或b= ，
所以答案是：或b=