Question

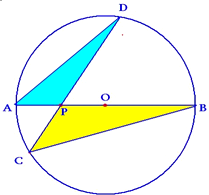如图，已知AB为圆O的直径，点P为AO的中点，CD为过P的任一条弦，则

S△CPB

S△APD

的取值范围为

 

．

Answer 1

考点：相似三角形的性质,圆周角定理

专题：推理和证明

分析：设出圆的半径，利用相交弦定理以及三角形的面积公式得到

S△CPB

S△APD

的二次函数，求出范围即可．

解答：解：设圆的半径为2，则AP=1，PB=3，由相交弦定理可知AP•PB=CP•PD=3．

S△CPB

S△APD

=

1 2 CP•PBsin∠CPB

1 2 AP•PDsin∠APD

=

3CP

PD

=

9

PD2

，PD∈（AP，PB），即PD∈（1，3）．
∴

S△CPB

S△APD

∈（1，3）．
故答案为：（1，3）．

点评：本题考查相交弦定理的应用三角形面积的求法，考查计算能力．