题目内容
(x2+
)6中x3的系数为( )
| 1 |
| x |
| A、20 | B、30 | C、25 | D、40 |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,令x的幂指数等于3,求出r的值,即可求得展开式中x3的系数.
解答:解:(x2+
)6展开式的通项公式为 Tr+1=
•x12-3r,
令12-3r=3,求得 r=3,可得展开式中x3的系数为
=20,
故选:A.
| 1 |
| x |
| C | r 6 |
令12-3r=3,求得 r=3,可得展开式中x3的系数为
| C | 3 6 |
故选:A.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
函数f(x)=-x3+3x2-4的单调递增区间是( )
| A、(-∞,0) | B、(-2,0) | C、(0,2) | D、(2,+∞) |
复数
(i为虚数单位)在复平面上对应的点在( )
| 2+i |
| i3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设a=
(1-2x)dx,则二项式(x2+
)6的常数项是( )
| ∫ | 2 0 |
| a |
| x |
| A、-240 | B、240 |
| C、-160 | D、160 |
已知数列{an},若点{n,an}(n∈N*)在直线y+2=k(x-5)上,则数列{an}的前9项和S9=( )
| A、18 | B、-45 | C、22 | D、-18 |
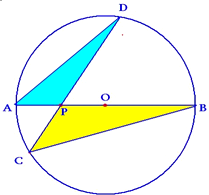 如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则
如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则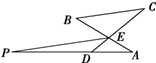 如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.
如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.