题目内容
在(x2-
)5的展开式中,x的系数为( )
| 1 |
| x |
| A、10 | B、-10 |
| C、20 | D、-20 |
考点:二项式系数的性质
专题:二项式定理
分析:由题意,可先由公式得出二项展开式的通项Tr+1=
•(-1)rx10-3r,再令10-3r=1,得r=3即可得出x项的系数.
| C | r 5 |
解答:解:(x2-
)5的二项展开式的通项为Tr+1=
•(x2)5-r(-
)r=
•(-1)rx10-3r,
令10-3r=1,得r=3,
故x项的系数为
•(-1)3=-10,
故选:B.
| 1 |
| x |
| C | r 5 |
| 1 |
| x |
| C | r 5 |
令10-3r=1,得r=3,
故x项的系数为
| C | 3 5 |
故选:B.
点评:本题考查二项式的通项公式,熟练记忆公式是解题的关键,求指定项的系数是二项式考查的一个重要题型,是高考的热点,要熟练掌握.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
已知f(x)=3x2+5,则从0.1到0.2的平均变化率为( )
| A、0.3 | B、0.6 | C、0.9 | D、1.2 |
若复数z1=1+2i,z2=1-i,其中i是虚数单位,则(z1+z2)i在复平面内对应的点在( )
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |
(1-2x)6的展开式中x2项的系数是( )
| A、12 | B、54 | C、60 | D、160 |
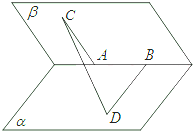 如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=2,AC=3,BD=4,求CD的长.
如图,60°的二面角的棱上有A、B两点,直线AC、BD分别在这个二面角的两个半平面内,且都垂直于AB.已知AB=2,AC=3,BD=4,求CD的长.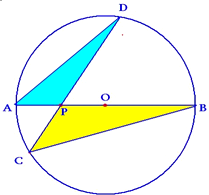 如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则
如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则