题目内容
在△ABC中,O是其外接圆的圆心,其两条中线的交点是G,两条高线的交点是H,设OG=λGH,则λ的值为 .
考点:圆內接多边形的性质与判定
专题:直线与圆
分析:取特殊值,假设△ABC是直角三角形,∠ABC=90°,由重心性质得OG=
GH,又OG=λGH,所以λ=
.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:取特殊值,假设△ABC是直角三角形,∠ABC=90°,如图,
解:取特殊值,假设△ABC是直角三角形,∠ABC=90°,如图,
AC边的中点O是其外接圆的圆心,两条中线BO,AD交于点G,
则G是△ABC的重心,两条高线AB,CB交于H,H与B重合,
则由重心性质得OG=
GH,
又OG=λGH,所以λ=
.
故答案为:
.
 解:取特殊值,假设△ABC是直角三角形,∠ABC=90°,如图,
解:取特殊值,假设△ABC是直角三角形,∠ABC=90°,如图,AC边的中点O是其外接圆的圆心,两条中线BO,AD交于点G,
则G是△ABC的重心,两条高线AB,CB交于H,H与B重合,
则由重心性质得OG=
| 1 |
| 2 |
又OG=λGH,所以λ=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查实数值的求法,是基础题,解题时要认真审题,注意特殊值法的合理运用.

练习册系列答案
相关题目
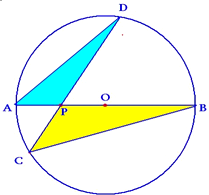 如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则
如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则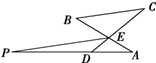 如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.
如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.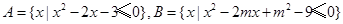 ,
,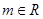 .
.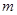 = 3,求
= 3,求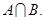 ;
;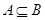 ,求实数
,求实数