题目内容
设函数f(x)=(x-1)kcosx(k=1,2),则( )
| A、当k=1时,f(x)在x=1处取得极小值 | B、当k=1时,f(x)在x=1处取得极大值 | C、当k=2时,f(x)在x=1处取得极小值 | D、当k=2时,f(x)在x=1处取得极大值 |
考点:利用导数研究函数的极值
专题:导数的综合应用
分析:求导函数,确定函数的单调性,从而可得函数的极值.
解答:解:∵f(x)=(x-1)kcosx,
∴当k=1时,f(x)=(x-1)cosx,
∴f′(x)=cosx-(x-1)sinx,
当x=1时,f′(1)=cos1≠0,
此时f(1)不是极值,故A,B错误.
当k=2时,f(x)=(x-1)2cosx,
∴f′(x)=2(x-1)cosx-(x-1)2sinx,
当x=1时,f′(1)=0,
故当x→1+时,f′(x)>0,当x→1-时,f′(x)<0,
故f(x)在x=1处取得极小值.
故选:C
∴当k=1时,f(x)=(x-1)cosx,
∴f′(x)=cosx-(x-1)sinx,
当x=1时,f′(1)=cos1≠0,
此时f(1)不是极值,故A,B错误.
当k=2时,f(x)=(x-1)2cosx,
∴f′(x)=2(x-1)cosx-(x-1)2sinx,
当x=1时,f′(1)=0,
故当x→1+时,f′(x)>0,当x→1-时,f′(x)<0,
故f(x)在x=1处取得极小值.
故选:C
点评:本题考查导数知识的运用,考查函数的单调性与最值,综合性较强.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
下列有关命题的说法正确的是( )
| A、命题“x2=1,则x=1”的否命题为“若x2=1,则x≠1” | B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” | C、若“p∨q”为真命题,则p,q至少有一个为真命题 | D、命题“若x=y,则sinx=siny”的逆命题为假命题 |
已知双曲线
-
=1(a>0,b>0)的一条渐近线方程是y=
x,它的一个焦点在抛物线y2=48x的准线上,则双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知f(x)=3x2+5,则从0.1到0.2的平均变化率为( )
| A、0.3 | B、0.6 | C、0.9 | D、1.2 |
函数f(x)=-x3+3x2-4的单调递增区间是( )
| A、(-∞,0) | B、(-2,0) | C、(0,2) | D、(2,+∞) |
已知回归直线的斜率的估计值是1.2,样本点的中心为(4,5),则回归直线方程是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若复数z1=1+2i,z2=1-i,其中i是虚数单位,则(z1+z2)i在复平面内对应的点在( )
| A、第一象限 | B、第二象限 | C、第三象限 | D、第四象限 |

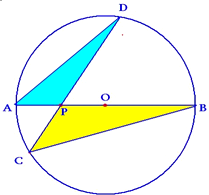 如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则
如图,已知AB为圆O的直径,点P为AO的中点,CD为过P的任一条弦,则