题目内容
4.全集U={1,2,3,4,5,6,7,8,9},(∁UA)∪∁UB={2,3,4,6,7,8},(∁UA)∩B={3,7},(∁UA)∪B={1,3,5,6,7,8,9}.求A,B.分析 根据Venn图进行求解即可.
解答 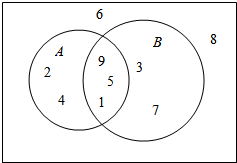 解:∵(∁UA)∪∁UB=∁U(A∩B)={2,3,4,6,7,8},
解:∵(∁UA)∪∁UB=∁U(A∩B)={2,3,4,6,7,8},
∴A∩B={1,5,9}
∵(∁UA)∩B={3,7},
∴3,7∈B,即B={1,3,5,7,9}.
∵(∁UA)∪B={1,3,5,6,7,8,9}.
∴A={1,2,4,5,9}.
对应的Venn图为:
点评 本题主要考查集合的基本运算,根据Venn图表示集合关系是解决本题的关键.

练习册系列答案
相关题目
15.已知a<b<0,奇函数f(x)在[-b,-a]上单调递减,且f(x)>0,那么在[a,b]上,g(x)=$\frac{1}{f(x)}$ ( )
| A. | 单调递增,且g(x)>0 | B. | 单调递减,且g(x)<0 | C. | 单调递增,且g(x)<0 | D. | 单调递减,且g(x)>0 |
9.已知函数f(x)满足f(x+1)=-f(x),且f(x)是偶函数,当x∈[0,1]时,f(x)=x2,若在区间[-1,3]内,函数g(x)=f(x)-k有4个零点,则实数k的取值范围是( )
| A. | [$\frac{1}{4}$,$\frac{1}{3}$) | B. | (0,$\frac{1}{2}$) | C. | (0,1) | D. | ($\frac{1}{3}$,$\frac{1}{2}$) |
16.函数f(x)在点x0处有定义,是当x→x0时f(x)有极限的( )
| A. | 必要条件 | B. | 充分条件 | C. | 充要条件 | D. | 无关条件 |