题目内容
13．函数f（x）=ax2-2ax+1（a＜0）在[0，3]上的最大值为2，则函数f（x）在[0，3]的最小值为-2．分析 配方，利用函数f（x）=ax2-2ax+1（a＜0）在[0，3]上的最大值为2，求出a，即可求出函数f（x）在[0，3]的最小值．
解答 解：f（x）=ax2-2ax+1=a（x-1）2-a+1（a＜0）
∵f（x）=ax2-2ax+1（a＜0）在[0，3]上的最大值为2，
∴-a+1=2，
∴a=-1，
∴函数f（x）在[0，3]的最小值为f（3）=-9+6+1=-2，
故答案为：-2．
点评 本题考查二次函数在闭区间上的最值，考查学生的计算能力，正确配方是关键．
练习册系列答案
相关题目
3．函数y=$\frac{2x}{lnx}$的图象大致为（ ）
| A． |  | B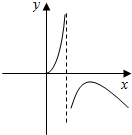． |  | C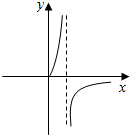． |  | D． |  |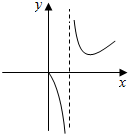
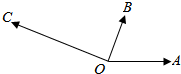如图，|$\overrightarrow{OA}$|=|$\overrightarrow{OB}$|=1，|$\overrightarrow{OC}$|=$\sqrt{3}$，∠AOB=60°，$\overrightarrow{OB}⊥\overrightarrow{OC}$，设$\overrightarrow{OC}=x\overrightarrow{OA}$+y$\overrightarrow{OB}$，则x，y的值分别为（ ）