题目内容
(12分)在平面直角坐标系xOy中,已知三点A(-1,0),B(1,0),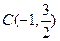 ,以A、B为焦点的椭圆经过点C。
,以A、B为焦点的椭圆经过点C。
(I)求椭圆的方程;
(II)设点D(0,1),是否存在不平行于x轴的直线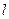 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使
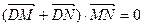 ?若存在,求出直线
?若存在,求出直线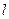 斜率的取值范围;若不存在,请说明理由:
斜率的取值范围;若不存在,请说明理由:
(III)对于y轴上的点P(0,n)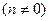 ,存在不平行于x轴的直线
,存在不平行于x轴的直线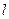 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使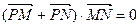 ,试求实数n的取值范围。
,试求实数n的取值范围。
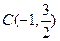 ,以A、B为焦点的椭圆经过点C。
,以A、B为焦点的椭圆经过点C。(I)求椭圆的方程;
(II)设点D(0,1),是否存在不平行于x轴的直线
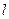 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使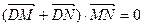 ?若存在,求出直线
?若存在,求出直线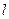 斜率的取值范围;若不存在,请说明理由:
斜率的取值范围;若不存在,请说明理由:(III)对于y轴上的点P(0,n)
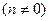 ,存在不平行于x轴的直线
,存在不平行于x轴的直线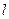 与椭圆交于不同两点M、N,使
与椭圆交于不同两点M、N,使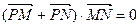 ,试求实数n的取值范围。
,试求实数n的取值范围。(1)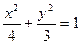 (2)不存在(3)
(2)不存在(3)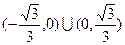
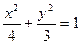 (2)不存在(3)
(2)不存在(3)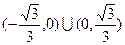
(I)设椭圆方程为 ,
,
据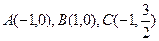 知,
知,
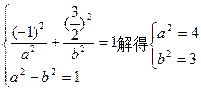
∴所求椭圆方程为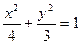 …………4分
…………4分
(II)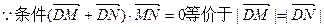
∴若存在符合条件的直线,该直线的斜率一定存在,
否则与点D(0,1)不在x轴上矛盾。
∴可设直线
由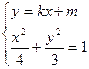 得
得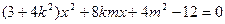
由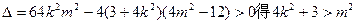 …………6分
…………6分
设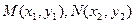 ,
,
MN的中点为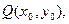
则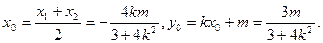
又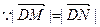
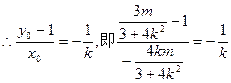
解得: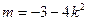 …………8分
…………8分
(将点的坐标代入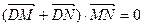 亦可得到此结果
亦可得到此结果 )
)
由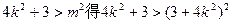 得,
得,
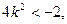 这是不可能的。
这是不可能的。
故满足条件的直线不存在。 …………9分
(III)据(II)有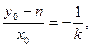
可推出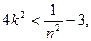 要使k存在,只需
要使k存在,只需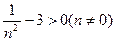
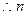 的取值范围是
的取值范围是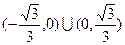 …………12分
…………12分
 ,
,据
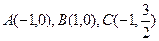 知,
知,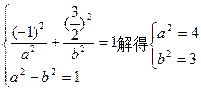
∴所求椭圆方程为
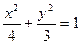 …………4分
…………4分(II)
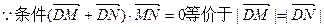
∴若存在符合条件的直线,该直线的斜率一定存在,
否则与点D(0,1)不在x轴上矛盾。
∴可设直线

由
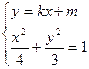 得
得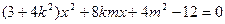
由
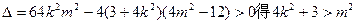 …………6分
…………6分设
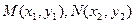 ,
,MN的中点为
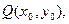
则
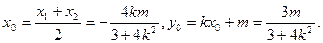
又
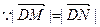
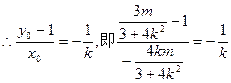
解得:
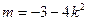 …………8分
…………8分(将点的坐标代入
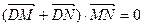 亦可得到此结果
亦可得到此结果 )
)由
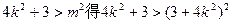 得,
得,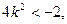 这是不可能的。
这是不可能的。故满足条件的直线不存在。 …………9分
(III)据(II)有
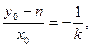
可推出
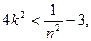 要使k存在,只需
要使k存在,只需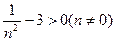
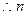 的取值范围是
的取值范围是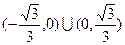 …………12分
…………12分
练习册系列答案
相关题目
 上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。
上任意一点,过点M引抛物线E的两条切线分别交x轴于点S , T,切点分别为B、A。 上移动时,直线AB恒过焦点F,求
上移动时,直线AB恒过焦点F,求 的值。
的值。
 抛物线
抛物线
 是C1的任意两条互相垂直的切线,并设
是C1的任意两条互相垂直的切线,并设 ,证明
,证明 :点M的纵坐标为定值;
:点M的纵坐标为定值;
 上一点
上一点 处的切线方程为
处的切线方程为 ”,类比也有结论:“椭圆
”,类比也有结论:“椭圆 处的切线方程为
处的切线方程为 ”,过椭圆C:
”,过椭圆C: 的右准线l上任意一点M引椭圆C的两条切线,切点为 A、B.
的右准线l上任意一点M引椭圆C的两条切线,切点为 A、B.  的直线
的直线 过椭圆
过椭圆 的右焦点,则
的右焦点,则



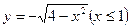 的长度是 .
的长度是 .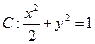 的左焦点为
的左焦点为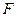 ,左准线为
,左准线为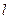 ,点
,点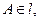 线段
线段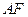 交椭圆
交椭圆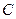 于点
于点 ,若
,若 ,则
,则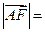 _____________.
_____________.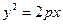
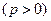 与双曲线
与双曲线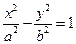
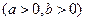 有相同的焦点
有相同的焦点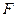 ,点
,点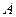 是两曲线的一个交点,且
是两曲线的一个交点,且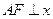 轴,若
轴,若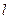 为双曲线的一条渐近线,则
为双曲线的一条渐近线,则


