题目内容

【题目】如图，在三棱锥A﹣BCD中，侧面ABC是一个等腰直角三角形，∠BAC=90°，底面BCD是一个等边三角形，平面ABC⊥平面BCD，E为BD的中点，则AE与平面BCD所成角的大小为 ．

【答案】45°
【解析】解：∵在三棱锥A﹣BCD中，侧面ABC是一个等腰直角三角形，∠BAC=90°，
底面BCD是一个等边三角形，平面ABC⊥平面BCD，E为BD的中点，
∴过A作AO⊥平面BDC，交BC于O，连结OE，则O是BC中点，
∠AEO是AE与平面BCD所成角，
∵△ABC是等腰直角三角形，O是BC中点，E是BD中点，△BDC是等边三角形，
∴AO=OE，∴∠AEO=45°．
∴AE与平面BCD所成角的大小为45°．
所以答案是：45°．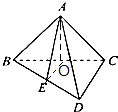

【考点精析】利用空间角的异面直线所成的角对题目进行判断即可得到答案，需要熟知已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则．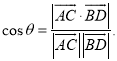

练习册系列答案
相关题目

【题目】设函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，﹣ ＜φ＜ ，x∈R）的部分图象如图所示．
（Ⅰ）求函数y=f（x）的解析式；
（Ⅱ）将函数y=f（x）的图象沿x轴方向向右平移 个单位长度，再把横坐标缩短到原来的 （纵坐标不变），得到函数y=g（x）的图象，当x∈[﹣ ， ]时，求函数g（x）的值域．

【题目】已知函数f（x）=loga ，g（x）=loga（x+2a）+loga（4a﹣x），其中a＞0，且a≠1．
（1）求f（x）的定义域，并判断f（x）的奇偶性；
（2）已知区间D=[2a+1，2a+ ]满足3aD，设函数h（x）=f（x）+g（x），h（x）的定义域为D，若对任意x∈D，不等式|h（x）|≤2恒成立，求实数a的取值范围．

【题目】已知函数f（x）=（ ）x的图象与函数y=g（x）的图象关于直线y=x对称，令h（x）=g（1﹣x2），则关于函数y=h（x）的下列4个结论： ①函数y=h（x）的图象关于原点对称；
②函数y=h（x）为偶函数；
③函数y=h（x）的最小值为0；
④函数y=h（x）在（0，1）上为增函数
其中，正确结论的序号为 ． （将你认为正确结论的序号都填上）

【题目】已知f（x）=|x|（2﹣x）
（1）作出函数f（x）的大致图象，并指出其单调区间；
（2）若函数f（x）=c恰有三个不同的解，试确定实数c的取值范围．

【题目】已知函数f（x）=b+logax（x＞0且a≠1）的图象经过点（8，2）和（1，﹣1）．
（1）求f（x）的解析式；
（2）[f（x）]2=3f（x），求实数x的值；
（3）令y=g（x）=2f（x+1）﹣f（x），求y=g（x）的最小值及其最小值时x的值．

【题目】已知椭圆的中心在原点，焦点为 ，且离心率 ．
（1）求椭圆的方程；
（2）求以点P（2，﹣1）为中点的弦所在的直线方程．

【题目】求满足下列条件的曲线方程：
（1）经过两条直线2x+y﹣8=0和x﹣2y+1=0的交点，且垂直于直线6x﹣8y+3=0的直线
（2）经过点C（﹣1，1）和D（1，3），圆心在x轴上的圆．

【题目】已知椭圆C： （a＞b＞0）的左、右焦点为F1（﹣2，0），F2（2，0），点M（﹣2， ） 在椭圆C上．
（1）求椭圆C的标准方程；
（2）已知斜率为k的直线l过椭圆C的右焦点F2 ， 与椭圆C相交于A，B两点．
①若|AB|= ，求直线l的方程；
②设点P（ ，0），证明： 为定值，并求出该定值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网