题目内容
已知条件p: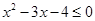 ;条件q:
;条件q: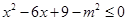 ,若p是q的充分不必要条件,则m的取值范围是( )
,若p是q的充分不必要条件,则m的取值范围是( )
A.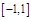 | B.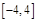 | C.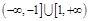 | D.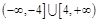 |
D
解析试题分析:对于命题p:∵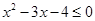 ,∴
,∴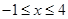 ,对于命题q:∵
,对于命题q:∵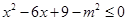 ,∴
,∴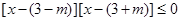 ,∴
,∴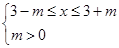 或
或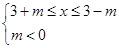 ,又p是q的充分不必要条件,∴
,又p是q的充分不必要条件,∴ 或
或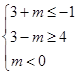 ,解得
,解得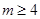 或
或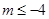 ,即m的取值范围为
,即m的取值范围为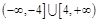 ,故选D
,故选D
考点:本题考查了充要条件的判断
点评:利用充要条件的概念转化为集合的子集关系,从而利用数轴解决此类问题的关键

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
下列关于命题的说法中错误的是( )
A.对于命题P: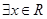 ,使得 ,使得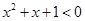 ,则 ,则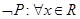 ,则 ,则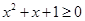 |
B.“ ”是“ ”是“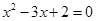 ”的充分不必要条件 ”的充分不必要条件 |
C.命题“若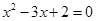 ,则 ,则 ”的逆否命题是:“若 ”的逆否命题是:“若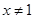 ,则 ,则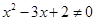 ” ” |
D.若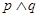 为假命题,则 为假命题,则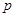 、 、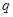 均为假命题 均为假命题 |
给出下面结论:
(1)命题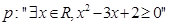 的否定为
的否定为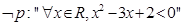 ;
;
(2)若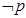 是
是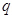 的必要不充分条件,则
的必要不充分条件,则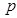 是
是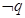 的充分不必要条件;
的充分不必要条件;
(3)“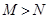 ”是“
”是“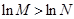 ”成立的充分不必要条件;
”成立的充分不必要条件;
(4) 若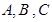 是
是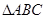 的三个内角,则“
的三个内角,则“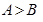 ”是“
”是“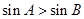 ”成立的充要条件。
”成立的充要条件。
其中正确结论的个数是
| A.4 | B.3 | C.2 | D.1 |
设a、b、c∈R+,P=a+b-c,Q=b+c-a,R=c+a-b,则“PQR>0”是“P、Q、R同时大于零”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题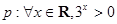 ,则( )
,则( )
A.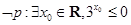 | B.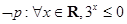 |
C. | D.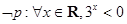 |
对于任意实数 ,<
,< >表示不小于
>表示不小于 的最小整数,例如<1.1>=2,<
的最小整数,例如<1.1>=2,<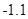 >=
>= 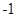 ,那么“
,那么“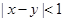 ”是“<
”是“< >=<
>=<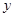 >”( ).
>”( ).
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知三个命题:①方程x2-x+2=0的判别式小于或等于零;②若|x|≥0,则x≥0;③5>2且3<7.其中真命题是
| A.①和② | B.①和③ | C.②和③ | D.只有① |
设α、β是两个不同的平面,l、m为两条不同的直线,命题p:若α∥β,l?α,m?β则l∥m;命题q:l∥α,m⊥l,m?β,则α⊥β.则下列命题为真命题的是( )
| A.p或q | B.p且q |
| C.非p或q | D.p且非q |
若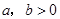 ,则
,则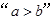 是“
是“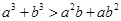 ”的( )
”的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充分且必要条件 | D.既非充分也非必要条件 |