题目内容
设a、b、c∈R+,P=a+b-c,Q=b+c-a,R=c+a-b,则“PQR>0”是“P、Q、R同时大于零”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
C
解析试题分析:根据题意,由于a、b、c∈R+,P=a+b-c,Q=b+c-a,R=c+a-b,,如果“PQR>0”则说明可能都是大于零,或者有两个为负数,一个为正数,但是假设两个为负数a+b-c<0, b+c-a<0,相加得到b<0,则可以推出三个都为负数,故只有前者,因此说条件是结论成立的充要条件,选C.
考点:充分条件
点评:解决的关键是根据不等式 性质来分析a,b,c的符号与P,Q,R的的关系,属于基础题。

练习册系列答案
相关题目
“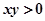 ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
可导函数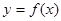 在一点的导数值为
在一点的导数值为 是函数
是函数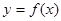 在这点取极值的( )
在这点取极值的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知圆 的极坐标方程为
的极坐标方程为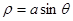 ,则“
,则“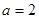 ”是“圆
”是“圆 与极轴所在直线相切”的 ( )
与极轴所在直线相切”的 ( )
| A.充分不必要条件. | B.必要不充分条件. |
| C.充要条件. | D.既不充分又不必要条件. |
已知条件p: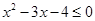 ;条件q:
;条件q: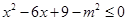 ,若p是q的充分不必要条件,则m的取值范围是( )
,若p是q的充分不必要条件,则m的取值范围是( )
A.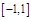 | B.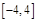 | C.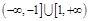 | D.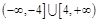 |
已知命题p: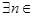 N
N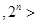 1 000,则
1 000,则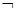 p为( )
p为( )
A.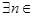 N N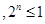 000 000 | B.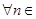 N N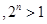 000 000 |
C.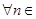 N N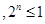 000 000 | D.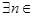 N N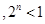 000 000 |
若实数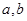 满足
满足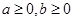 且
且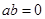 ,则称
,则称 与
与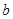 互补.记
互补.记 ,那么
,那么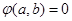 是
是 与
与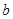 互补的 ( ) 条件
互补的 ( ) 条件
| A.必要不充分 | B.充分而不必要 | C.充要 | D.既不充分也不必要 |
命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是
| A.若f(x) 是偶函数,则f(-x)是偶函数 |
| B.若f(x)不是奇函数,则f(-x)不是奇函数 |
| C.若f(-x)是奇函数,则f(x)是奇函数 |
| D.若f(-x)不是奇函数,则f(x)不是奇函数 |
 R,则a>2是(a-1)(a-2)>0的
R,则a>2是(a-1)(a-2)>0的