题目内容
【题目】已知
，
是两条不同直线，
，
是两个不同平面，给出下列四个命题：
①若，垂直于同一平面，则与平行；
②若，平行于同一平面，则与平行；
③若，不平行，则在内不存在与平行的直线；
④若，不平行，则与不可能垂直于同一平面
其中真命题的个数为（ ）
A.4B.3C.2D.1
【答案】D
【解析】
①若
垂直于同一平面，则
与
可能相交；②若
，
平行于同一平面，则两直线位置不能确定；③若相交，则在内存在无数条与平行的直线；④用反证法证明结论成立.即可得出结论.
①若直线
垂直平面
，根据面面垂直的判断定理，
所有过直线的平面都与平面垂直，取其中的两个平面为，
此时相交，故①不正确；
②若，平行于同一平面，则两直线可能平行、相交、异面；
故②不正确；
③若不平行，则相交，则在内存在无数条直线与两平面的交线平行，
根据线面平面的判定定理，这无数条平行线与平面平行，故③不正确；
④假设
同垂直平面，则有
，与已知不平行矛盾，
故假设不成立，即不同垂直平面，故④正确.
故选:D.
鸿图图书寒假作业假期作业吉林大学出版社系列答案
【题目】某市为创建全国文明城市，推出“行人闯红灯系统建设项目”，将针对闯红灯行为进行曝光.交警部门根据某十字路口以往的监测数据，从穿越该路口的行人中随机抽查了
人，得到如图示的列联表：
闯红灯 | 不闯红灯 | 合计 | |
年龄不超过 |
|
|
|
年龄超过 |
|
|
|
合计 |
|
|
|
（1）能否有
的把握认为闯红灯行为与年龄有关？
（2）下图是某路口监控设备抓拍的
个月内市民闯红灯人数的统计图.请建立
与
的回归方程
，并估计该路口
月份闯红灯人数.
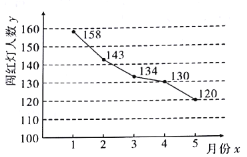
附：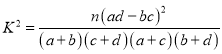
，
|
|
|
|
|
|
|
|
|
|
|
|
参考数据：
，
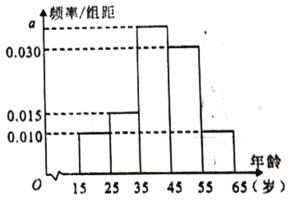
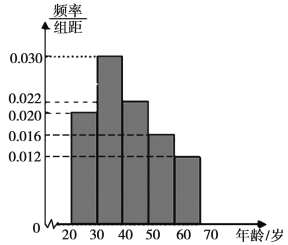
【题目】某知名电商在
双十一购物狂欢节中成交额再创新高，
月日单日成交额达
亿元.某店主在此次购物狂欢节期间开展了促销活动，为了解买家对此次促销活动的满意情况，随机抽取了参与活动的
位买家，调查了他们的年龄层次和购物满意情况，得到年龄层次的频率分布直方图和“购物评价为满意”的年龄层次频数分布表.年龄层次的频率分布直方图：
“购物评价为满意”的年龄层次频数分布表：
年龄（岁） |
|
|
|
|
|
频数 |
|
|
|
|
|
（1）估计参与此次活动的买家的平均年龄（同一组中的数据用该组区间的中点值做代表）；
（2）若年龄在
岁以下的称为“青年买家”，年龄在岁以上（含岁）的称为“中年买家”，完成下面的列联表，并判断能否有
的把握认为中、青年买家对此次活动的评价有差异？
评价满意 | 评价不满意 | 合计 | |
中年买家 | |||
青年买家 | |||
合计 |
|
附：参考公式：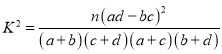
.
|
|
|
|
|
|
|
|
