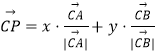Question

【题目】如图，已知三棱柱的所有棱长都相等，且侧棱垂直于底面，由沿棱柱侧面经过棱到点的最短路线长为，设这条最短路线与的交点为．

（1）求三棱柱的体积；

（2）证明：平面平面．

Answer 1

【答案】（1） （2）详见解析

【解析】试题分析：（1）由题意求出棱长，再求出三棱柱ABC-A1B1C1的底面面积，再求出高AA1，即可求出棱柱的体积．（2）连接AD，B1D，平面A1BD内的直线OD垂直平面A1ABB1内的两条相交直线A1B，AB1，即可证明平面A1BD⊥平面A1ABB1．

试题解析：

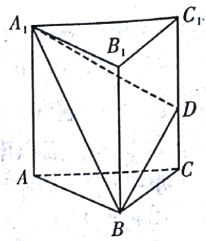
(1)如图，将侧面绕棱旋转使其与侧面在同一平面上，点运动到点的位置，连接，则就是由点沿棱柱侧面经过棱到点的最短路线．

设棱柱的棱长为，则，

∵，∴为的中点，

在中，由勾股定理得，

即解得，

∵，

∴．

（2）设与的交点为，连结，

∵，

∴，∴，

∵，∴平面．

又∵平面，∴平面平面．