题目内容
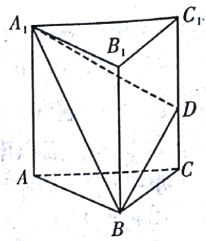
【题目】如图,已知三棱柱![]() 的所有棱长都相等,且侧棱垂直于底面,由
的所有棱长都相等,且侧棱垂直于底面,由![]() 沿棱柱侧面经过棱
沿棱柱侧面经过棱![]() 到点
到点![]() 的最短路线长为
的最短路线长为![]() ,设这条最短路线与
,设这条最短路线与![]() 的交点为
的交点为![]() .
.

(1)求三棱柱![]() 的体积;
的体积;
(2)证明:平面![]() 平面
平面![]() .
.
【答案】(1)![]() (2)详见解析
(2)详见解析
【解析】试题分析:(1)由题意求出棱长,再求出三棱柱ABC-A1B1C1的底面面积,再求出高AA1,即可求出棱柱的体积.(2)连接AD,B1D,平面A1BD内的直线OD垂直平面A1ABB1内的两条相交直线A1B,AB1,即可证明平面A1BD⊥平面A1ABB1.
试题解析:
(1)如图,将侧面![]() 绕棱
绕棱![]() 旋转
旋转![]() 使其与侧面
使其与侧面![]() 在同一平面上,点
在同一平面上,点![]() 运动到点
运动到点![]() 的位置,连接
的位置,连接![]() ,则
,则![]() 就是由点
就是由点![]() 沿棱柱侧面经过棱
沿棱柱侧面经过棱![]() 到点
到点![]() 的最短路线.
的最短路线.
设棱柱的棱长为![]() ,则
,则![]() ,
,
∵![]() ,∴
,∴![]() 为
为![]() 的中点,
的中点,
在![]() 中,由勾股定理得
中,由勾股定理得![]() ,
,
即![]() 解得
解得![]() ,
,
∵![]() ,
,
∴![]() .
.
(2)设![]() 与
与![]() 的交点为
的交点为![]() ,连结
,连结![]() ,
,
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
又∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.


练习册系列答案
相关题目
【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:
(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注: ![]()