题目内容
函数y=cos3x+sin2x-cosx的最大值等于

试题分析:将函数y=cos3x+sin2x-cosx转化为y=cos3x-cos2x-cosx+1,利用基本不等式即可求得答案.解:∵y=cos3x+sin2x-cosx=cos3x-cos2x-cosx+1=cos2x(cosx-1)+(1-cosx)=(1-cosx)(1-cos2x),=(1-cosx)(1-cosx)(1+cosx)=
 (1-cosx)(1-cosx)(2+2cosx),∵1-cosx≥0,2+2cosx≥0,∴(1-cosx)(1-cosx)(2+2cosx)
(1-cosx)(1-cosx)(2+2cosx),∵1-cosx≥0,2+2cosx≥0,∴(1-cosx)(1-cosx)(2+2cosx)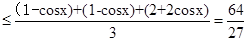 ,当且仅当1-cosx=2+2cosx,即cosx=-
,当且仅当1-cosx=2+2cosx,即cosx=-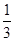
时取“=”. 函数y=cos3x+sin2x-cosx的最大值等于
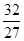 ,故答案为
,故答案为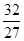 。
。点评:本题考查复合三角函数的单调性,着重考查基本不等式的应用,考查分析、转化与运算能力,属于中档题

练习册系列答案
相关题目
 的周期为
的周期为 ,
,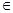 R,都有f(x)
R,都有f(x) ;
; 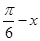 ),求函数g(x)的单调增区间.
),求函数g(x)的单调增区间. 图象的一部分如图所示,则其解析式为 .
图象的一部分如图所示,则其解析式为 .
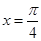 是函数
是函数 的一条对称轴,且
的一条对称轴,且 的最大值为
的最大值为 ,则函数
,则函数
 的图像的一条对称轴方程是( )
的图像的一条对称轴方程是( )



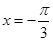
 的解集是 .
的解集是 .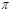 ,且在
,且在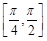 上单调递增的奇函数是 ( )
上单调递增的奇函数是 ( )



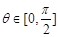 ,恒有
,恒有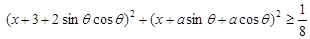 ,则实数a的取值范围为 .
,则实数a的取值范围为 . 的图象是把y=3cos3x的图象平移而得,平移方法是( )
的图象是把y=3cos3x的图象平移而得,平移方法是( ) 个单位长度
个单位长度 个单位长度
个单位长度