题目内容
对任意实数x和任意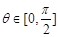 ,恒有
,恒有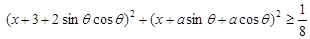 ,则实数a的取值范围为 .
,则实数a的取值范围为 .
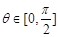 ,恒有
,恒有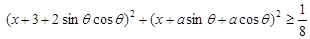 ,则实数a的取值范围为 .
,则实数a的取值范围为 .a≤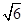 或a≥
或a≥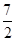 .
.
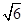 或a≥
或a≥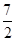 .
. 试题分析:
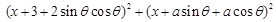 表示点A(x,x)与点B
表示点A(x,x)与点B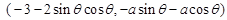 的距离的平方,又动点A(x,x)在直线y=x上,∵
的距离的平方,又动点A(x,x)在直线y=x上,∵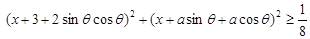 ,∴动点B在区域
,∴动点B在区域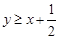 或
或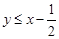 上.∴
上.∴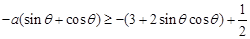 (1)或
(1)或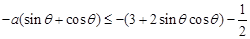 (2).对于(1):由题意
(2).对于(1):由题意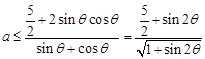 ,设t=
,设t=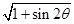 ,t∈[1,
,t∈[1,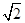 ],∴
],∴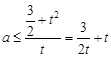 ,又
,又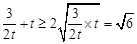 ,当
,当 时,等号成立,∴a≤
时,等号成立,∴a≤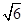 ;对于(2):由题意
;对于(2):由题意  ,又函数
,又函数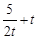 在t∈[1,
在t∈[1,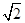 ]单调递减,故当
]单调递减,故当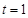 时,函数
时,函数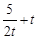 有最大值
有最大值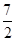 ,∴a≥
,∴a≥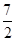 ,综上a的取值范围是a≤
,综上a的取值范围是a≤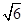 或a≥
或a≥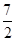
点评:若在等式或不等式中出现两个变量,其中一个变量的范围已知,另一个变量的范围为所求,且容易通过恒等变形将两个变量分别置于等号或不等号的两边,则可将恒成立问题转化成函数的最值问题求解。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ,
, ]上的图像,
]上的图像,
 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍,
倍,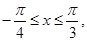 则函数
则函数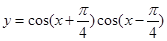 的值域为________.
的值域为________.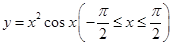 的图象是
的图象是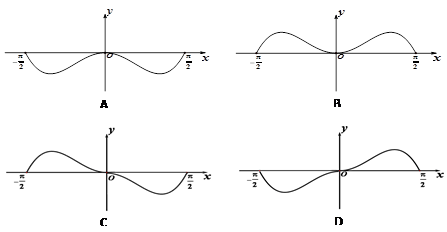
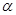 为第三象限角,
为第三象限角,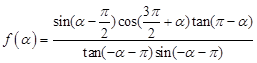 .
.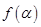 ;
;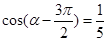 ,求
,求 的图象,只要将函数
的图象,只要将函数 的图象( )
的图象( )  单位
单位 单位
单位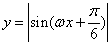 的最小正周期是
的最小正周期是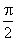 ,则正数
,则正数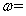 ______.
______. 的图象,只需把函数
的图象,只需把函数 的图象上所有的点 ( )
的图象上所有的点 ( ) 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 倍(纵坐标不变)
倍(纵坐标不变) 倍(纵坐标不变)
倍(纵坐标不变)