Question

【题目】已知抛物线的焦点为，平行于轴的两条直线分别交于两点，交的准线于两点 .

（1）若在线段上，是的中点，证明；

（2）若的面积是的面积的两倍，求中点的轨迹方程.

Answer 1

【答案】（1）证明见解析；（2）．

【解析】

试题分析：设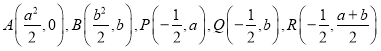的方程为

．（1）由在线段上，又 ；（2）设与轴的交点为 （舍去），．设满足条件的的中点为．当与轴不垂直时．当与轴垂直时与重合所求轨迹方程为．

试题解析：由题设，设，则，且

．

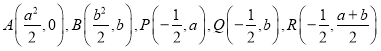记过两点的直线为，则的方程为．．．．．．．．．．．．．3分

（1）由于在线段上，故，

记的斜率为的斜率为，则，

所以．．．．．．．．．．．．．．．．．．5分

（2）设与轴的交点为，

则，

由题设可得，所以（舍去），．

设满足条件的的中点为．

当与轴不垂直时，由可得．

而，所以．

当与轴垂直时，与重合，所以，所求轨迹方程为 ．．．．．．．．．12分