题目内容
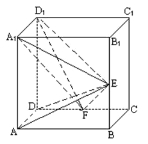
【题目】如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(Ⅰ)证明:AD⊥D1F;
(Ⅱ)求AE与D1F所成的角;
(Ⅲ)证明:面AED⊥面A1FD1.
【答案】(Ⅰ)详见解析(Ⅱ) 900(Ⅲ)详见解析
【解析】
试题分析:求解时可采用空间向量的方法,(Ⅰ)中可通过证明直线的方向向量垂直得到直线垂直;(Ⅱ)通过求直线的方向向量的夹角求解异面直线所成角;(Ⅲ)首先求解两平面的法向量,由法向量垂直证明平面垂直
试题解析:以D为原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系. 设正方体的棱长为1…………………………………1分
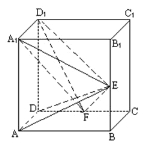
则有A(1,0,0),E(1,2,![]() ),F(0,
),F(0,![]() ,0),D1(0,0,1),
,0),D1(0,0,1),
A1(1,0,1)……2分
(Ⅰ)![]() ,∴AD⊥D1F………………………4分
,∴AD⊥D1F………………………4分
(Ⅱ)![]() ,∴AE⊥D1F
,∴AE⊥D1F
AE与D1F所成的角为900…………………………………………………………………7分
(Ⅲ)由(Ⅰ)、(Ⅱ)知:AD⊥D1F,AE⊥D1F,又AD![]() AE=A,
AE=A,
所以 D1F⊥平面AED,又D1F在平面A1FD1内,
所以面AED⊥面A1FD1……………………………………………………………………12分

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】重庆八中大学城校区与本部校区之间的驾车单程所需时间为![]() ,
,![]() 只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
只与道路畅通状况有关,对其容量为500的样本进行统计,结果如下:
| 25 | 30 | 35 | 40 |
频数(次) | 100 | 150 | 200 | 50 |
以这500次驾车单程所需时间的频率代替某人1次驾车单程所需时间的概率.
(1)求![]() 的分布列与
的分布列与![]() ;
;
(2)某天有3位教师独自驾车从大学城校区返回本部校区,记![]() 表示这3位教师中驾车所用时间少于
表示这3位教师中驾车所用时间少于![]() 的人数,求
的人数,求![]() 的分布列与
的分布列与![]() ;
;
(3)下周某天张老师将驾车从大学城校区出发,前往本部校区做一个50分钟的讲座,结束后立即返回大学城校区,求张老师从离开大学城校区到返回大学城校区共用时间不超过120分钟的概率.



