题目内容
已知命题P:关于x的方程x2-ax+4=0有实根;命题Q:关于x的函数y=2x2+ax+4在[3,+∞)上是增函数.若P或Q是真命题,P且Q是假命题,则实数a的取值范围是( )
| A.(-12,-4]∪[4,+∞) |
| B.[-12,-4]∪[4,+∞) |
| C.(-∞,-12)∪(-4,4) |
| D.[-12,+∞) |
C
【思路点拨】问题等价于命题P和Q一真一假,分类求解a的取值范围后求其并集即可.
解:命题P为真等价于Δ=a2-16≥0,解得a≤-4或a≥4;命题Q为真等价于- ≤3,a≥-12.P或Q是真命题,P且Q是假命题,则命题P和Q一真一假.当P真Q假时a<-12;当Q真P假时-4<a<4.故所求a的取值范围是(-∞,-12)∪(-4,4).
≤3,a≥-12.P或Q是真命题,P且Q是假命题,则命题P和Q一真一假.当P真Q假时a<-12;当Q真P假时-4<a<4.故所求a的取值范围是(-∞,-12)∪(-4,4).
解:命题P为真等价于Δ=a2-16≥0,解得a≤-4或a≥4;命题Q为真等价于-
 ≤3,a≥-12.P或Q是真命题,P且Q是假命题,则命题P和Q一真一假.当P真Q假时a<-12;当Q真P假时-4<a<4.故所求a的取值范围是(-∞,-12)∪(-4,4).
≤3,a≥-12.P或Q是真命题,P且Q是假命题,则命题P和Q一真一假.当P真Q假时a<-12;当Q真P假时-4<a<4.故所求a的取值范围是(-∞,-12)∪(-4,4).
练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
 >
> ,则a>b”,则( )
,则a>b”,则( )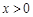 ,则
,则 ”的否命题为 .
”的否命题为 .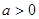 ,
,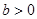 ,则有
,则有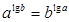 成立;
成立;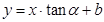 的倾斜角等于
的倾斜角等于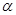 ;
;