题目内容
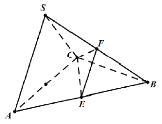
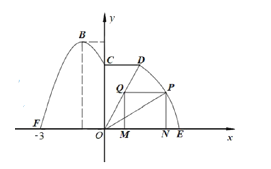
【题目】如图,要在河岸![]() 的一侧修建一条休闲式人行道,进行图纸设计时,建立了图中所示坐标系,其中
的一侧修建一条休闲式人行道,进行图纸设计时,建立了图中所示坐标系,其中![]() ,
,![]() 在
在![]() 轴上,且
轴上,且![]() ,道路的前一部分为曲线段
,道路的前一部分为曲线段![]() ,该曲线段为二次函数
,该曲线段为二次函数![]() 在
在![]() 时的图像,最高点为
时的图像,最高点为![]() ,道路中间部分为直线段
,道路中间部分为直线段![]() ,
,![]() ,且
,且![]() ,道路的后一段是以
,道路的后一段是以![]() 为圆心的一段圆弧
为圆心的一段圆弧![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的大小;
的大小;
(3)若要在扇形区域![]() 内建一个“矩形草坪”
内建一个“矩形草坪”![]() ,
,![]() 在圆弧
在圆弧![]() 上运动,
上运动,![]() 、
、![]() 在
在![]() 上,记
上,记![]() ,则当
,则当![]() 为何值时,“矩形草坪”面积最大.
为何值时,“矩形草坪”面积最大.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当
;(3)当![]() 时,矩形草坪面积最大.
时,矩形草坪面积最大.
【解析】
(1)将点![]() 的坐标代入函数
的坐标代入函数![]() 的解析式,可得出实数
的解析式,可得出实数![]() 的值;
的值;
(2)在函数![]() 的解析式中令
的解析式中令![]() ,可求出点
,可求出点![]() 的坐标,由此得出
的坐标,由此得出![]() ,可求出
,可求出![]() ,计算出
,计算出![]() ,由此可得出
,由此可得出![]() ;
;
(3)可得出![]() ,
,![]() ,从而得出“矩形草坪”的面积
,从而得出“矩形草坪”的面积![]() 关于
关于![]() 的表达式,利用三角恒等变换思想将
的表达式,利用三角恒等变换思想将![]() 关于
关于![]() 的表达式化简为
的表达式化简为![]() ,结合角
,结合角![]() 的范围,可计算出
的范围,可计算出![]() 的最大值以及对应的
的最大值以及对应的![]() 值.
值.
(1)由图可知函数![]() 的图象过点
的图象过点![]() ,
,
![]() ;
;
(2)由(1)知![]() ,当
,当![]() 时,
时,![]() ,
,![]() ,
,
又![]() 在
在![]() 中,
中,![]() ,
,![]() ;
;
(3)由(2)可知![]() 易知矩形草坪面积最大时,Q在OD上.
易知矩形草坪面积最大时,Q在OD上.
如图:![]() ,
,![]() ,
,![]() ,
,
又![]() ,
,![]()
![]() 矩形草坪的面积为:
矩形草坪的面积为:![]()
![]() ,
,
又![]() ,故当
,故当![]() 即
即![]() 时,有
时,有![]() .
.
综上所述,当![]() 时,矩形草坪面积最大.
时,矩形草坪面积最大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.