��Ŀ����
��������A=[0��3]��B=[0��3]���ֱ�Ӽ���A��B�и���ȡһ��Ԫ��m��n��������m��A��n��B����Ϊ��m��n����
������m��Z��n��Z��д�����еģ�m��n����ȡֵ����������¼�������
+
=1����Ӧ�����߱�ʾ������x���ϵ���Բ���ĸ��ʣ�
�������¼�������
+
=1����Ӧ�����߱�ʾ������x���ϵ���Բ���ҳ��᳤���ڶ��᳤��
�����ĸ��ʣ�
������m��Z��n��Z��д�����еģ�m��n����ȡֵ����������¼�������
| x2 |
| m+1 |
| y2 |
| n+1 |
�������¼�������
| x2 |
| m+1 |
| y2 |
| n+1 |
| 2 |
��������֪���еģ�m��n����ȡֵ���Ϊ����0��0������0��1������0��2������0��3������1��0������1��1������1��2������1��3������2��0������2��1������2��2������2��3������3��0������3��1����
��3��2������3��3����16�֣�
������
+
=1����Ӧ�����߱�ʾ������x���ϵ���Բ����m+1��n+1����m��n��
��Ӧ�ģ�m��n����ȡֵ���Ϊ����1��0������2��0������2��1������3��0������3��1������3��2����6�֣�
����¼�����Ϊ��P=
=
��
��������֪0��m��3��0��n��3����Բ����Ϊ2
������Ϊ2
��
��2
��
•2
����m��2n+1����������ͼ��ʾ��
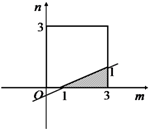
����¼�����ΪP=
=
��
��3��2������3��3����16�֣�
������
| x2 |
| m+1 |
| y2 |
| n+1 |
��Ӧ�ģ�m��n����ȡֵ���Ϊ����1��0������2��0������2��1������3��0������3��1������3��2����6�֣�
����¼�����Ϊ��P=
| 6 |
| 16 |
| 3 |
| 8 |
��������֪0��m��3��0��n��3����Բ����Ϊ2
| m+1 |
| n+1 |
��2
| m+1 |
| 2 |
| n+1 |

����¼�����ΪP=
| ||
| 3��3 |
| 1 |
| 9 |

��ϰ��ϵ�д�
�����Ŀ