题目内容
已知椭圆
+
=1(a>b>0)的焦点分别为F1,F2,若该椭圆上存在一点P使得∠F1PF2=60°,则椭圆离心率的取值范围是______.
| x2 |
| a2 |
| y2 |
| b2 |
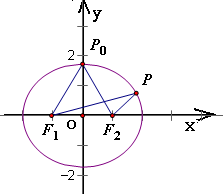
如图,当动点P在椭圆长轴端点处沿椭圆弧向短轴端点运动时,P对两个焦点的张角∠F1PF2渐渐增大,当且仅当P点位于短轴端点P0处时,张角∠F1PF2达到最大值.由此可得:
∵存在点P为椭圆上一点,使得∠F1PF2=60°,
∴△P0F1F2中,∠F1P0F2≥60°,
∴Rt△P0OF2中,∠OP0F2≥30°,
所以P0O≤
OF2,即b≤
c,
∴a2-c2≤3c2,可得a2≤4c2,
∴
≥
,
∵0<e<1,
∴
≤e<1.
故答案为:
≤e<1.
∵存在点P为椭圆上一点,使得∠F1PF2=60°,
∴△P0F1F2中,∠F1P0F2≥60°,
∴Rt△P0OF2中,∠OP0F2≥30°,
所以P0O≤
| 3 |
| 3 |
∴a2-c2≤3c2,可得a2≤4c2,
∴
| c |
| a |
| 1 |
| 2 |
∵0<e<1,
∴
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |


练习册系列答案
相关题目