题目内容
某工厂生产两批产品，第一批的10件产品中优等品有4件；第二批的5件产品中优等品有3件，现采用分层抽样方法从两批产品中共抽取3件进行质量检验．
（I）求从两批产品各抽取的件数；
（Ⅱ）记ξ表示抽取的3件产品中非优等品的件数，求ξ的分布列及数学期望．
（I）求从两批产品各抽取的件数；
（Ⅱ）记ξ表示抽取的3件产品中非优等品的件数，求ξ的分布列及数学期望．
（I）∵第一批有10件产品，第二批有5件产品，
现采用分层抽样方法从两批产品中共抽取3件进行质量检验，
∴每个个体被抽到的概率是
=
∴第一批应抽取
×10=2件，
第二批应抽取
×5=1件；
（Ⅱ）∵ξ表示抽取的3件产品中非优等品的件数，
∴ξ的可能取值为0，1，2，3
P（ξ=0）=
×
=
P（ξ=1）=
+
=
P（ξ=3）=
=
P（ξ=2）=1-P（ξ=0）-P（ξ=1）-P（ξ=3）=
∴ξ的分布列如下：
∴Eξ=0×
+1×
+2×
+3×
=
．
现采用分层抽样方法从两批产品中共抽取3件进行质量检验，
∴每个个体被抽到的概率是
| 3 |
| 10+5 |
| 1 |
| 5 |
∴第一批应抽取
| 1 |
| 5 |
第二批应抽取
| 1 |
| 5 |
（Ⅱ）∵ξ表示抽取的3件产品中非优等品的件数，
∴ξ的可能取值为0，1，2，3
P（ξ=0）=
| ||
|
| ||
|
| 6 |
| 75 |
P（ξ=1）=
| ||||||
|
| ||||
|
| 28 |
| 75 |
P（ξ=3）=
| ||||
|
| 10 |
| 75 |
P（ξ=2）=1-P（ξ=0）-P（ξ=1）-P（ξ=3）=
| 31 |
| 75 |
∴ξ的分布列如下：
∴Eξ=0×
| 6 |
| 75 |
| 28 |
| 75 |
| 31 |
| 75 |
| 10 |
| 75 |
| 8 |
| 5 |
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
的分布列P（
）=ak，k=1，2，3，4，5.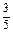
）；
＜
）.
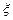的分布列和数学期望．
，则D(ξ)＝________.