题目内容
汽车租赁公司为了调查A,B两种车型的出租情况,现随机抽取了这两种车型各100辆汽车,分别统计了每辆车某个星期内的出租天数,统计数据如下表:
A型车
B型车
( I)从出租天数为3天的汽车(仅限A,B两种车型)中随机抽取一辆,估计这辆汽车恰好是A型车的概率;
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.
A型车
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
(Ⅱ)根据这个星期的统计数据,估计该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率;
(Ⅲ)如果两种车型每辆车每天出租获得的利润相同,该公司需要从A,B两种车型中购买一辆,请你根据所学的统计知识,给出建议应该购买哪一种车型,并说明你的理由.
( I)∵出租天数为3天的汽车A型车有30辆,B型车20辆.从中随机抽取一辆,这辆汽车是A型车的概率约为
=0.6.
( II)设“事件Ai表示一辆A型车在一周内出租天数恰好为i天”,
“事件Bj表示一辆B型车在一周内出租天数恰好为j天”,其中i,j=1,2,…,7.
则该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率为
P(A1B3+A2B2+A3B1)=P(A1B3)+P(A2B2)+P(A3B1)
=P(A1)P(B3)+P(A2)P(B2)+P(A3)P(B1)
=
×
+
×
+
×
=
.
该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率为
.
(Ⅲ)设X为A型车出租的天数,则X的分布列为
设Y为B型车出租的天数,则Y的分布列为
E(X)=1×0.05+2×0.10+3×0.30+4×0.35+5×0.15+6×0.03+7×0.02=3.62.
E(Y)=1×0.14+2×0.20+3×0.20+4×0.16+5×0.15+6×0.10+7×0.05=3.48.
一辆A类型的出租车一个星期出租天数的平均值为3.62天,B类车型一个星期出租天数的平均值为3.48天.
从出租天数的数据来看,A型车出租天数的方差大于B型车出租天数的方差,综合分析,选择A类型的出租车更加合理.
| 30 |
| 30+20 |
( II)设“事件Ai表示一辆A型车在一周内出租天数恰好为i天”,
“事件Bj表示一辆B型车在一周内出租天数恰好为j天”,其中i,j=1,2,…,7.
则该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率为
P(A1B3+A2B2+A3B1)=P(A1B3)+P(A2B2)+P(A3B1)
=P(A1)P(B3)+P(A2)P(B2)+P(A3)P(B1)
=
| 5 |
| 100 |
| 20 |
| 100 |
| 10 |
| 100 |
| 20 |
| 100 |
| 30 |
| 100 |
| 14 |
| 100 |
=
| 9 |
| 125 |
该公司一辆A型车,一辆B型车一周内合计出租天数恰好为4天的概率为
| 9 |
| 125 |
(Ⅲ)设X为A型车出租的天数,则X的分布列为
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 0.05 | 0.10 | 0.30 | 0.35 | 0.15 | 0.03 | 0.02 |
| Y | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| P | 0.14 | 0.20 | 0.20 | 0.16 | 0.15 | 0.10 | 0.05 |
E(Y)=1×0.14+2×0.20+3×0.20+4×0.16+5×0.15+6×0.10+7×0.05=3.48.
一辆A类型的出租车一个星期出租天数的平均值为3.62天,B类车型一个星期出租天数的平均值为3.48天.
从出租天数的数据来看,A型车出租天数的方差大于B型车出租天数的方差,综合分析,选择A类型的出租车更加合理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

 型血的人数占总人口数的比为
型血的人数占总人口数的比为 ,现从中随机抽取3人.
,现从中随机抽取3人. 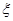 ,求
,求 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分)
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分) 的分布列和数学期望.
的分布列和数学期望.
 ,则
,则 .
. 的概率分布律如下表所示:
的概率分布律如下表所示:







 ,则
,则