题目内容
设离散型随机变量 的分布列P(
的分布列P( =
= )=ak,k=1,2,3,4,5.
)=ak,k=1,2,3,4,5.
(1)求常数a的值;
(2)求P( ≥
≥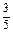 );
);
(3)求P( <
< <
< ).
).
 的分布列P(
的分布列P( =
= )=ak,k=1,2,3,4,5.
)=ak,k=1,2,3,4,5.(1)求常数a的值;
(2)求P(
 ≥
≥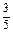 );
);(3)求P(
 <
< <
< ).
).(1) (2)
(2)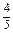 (3)
(3)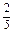
 (2)
(2)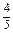 (3)
(3)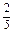
(1)由分布列的性质,得
a·1+a·2+a·3+a·4+a·5=1,
解得a= .
.
(2)由(1),得P( =
= )=
)= k,k=1,2,3,4,5.
k,k=1,2,3,4,5.
方法一 P( ≥
≥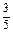 )=P(
)=P( =
=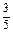 )+P(
)+P( =
=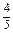 )+P(
)+P( =1)
=1)
= +
+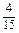 +
+ =
=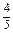 .
.
方法二 P( ≥
≥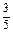 )=1-P(
)=1-P( <
<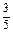 )
)
=1-[P( =
=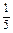 )+P(
)+P( =
=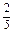 )]
)]
=1-(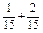 )=
)=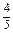 .
.
(3)∵ <
< <
< ,∴
,∴ =
=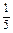 ,
,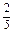 ,
,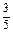 ,
,
∴P( <
< <
< )=P(
)=P( =
=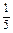 )+P(
)+P( =
=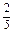 )+P(
)+P( =
=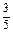 )
)
= +
+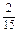 +
+ =
=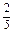 .
.
a·1+a·2+a·3+a·4+a·5=1,
解得a=
 .
.(2)由(1),得P(
 =
= )=
)= k,k=1,2,3,4,5.
k,k=1,2,3,4,5.方法一 P(
 ≥
≥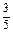 )=P(
)=P( =
=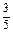 )+P(
)+P( =
=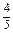 )+P(
)+P( =1)
=1)=
 +
+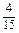 +
+ =
=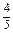 .
.方法二 P(
 ≥
≥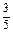 )=1-P(
)=1-P( <
<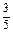 )
)=1-[P(
 =
=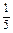 )+P(
)+P( =
=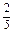 )]
)]=1-(
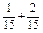 )=
)=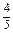 .
.(3)∵
 <
< <
< ,∴
,∴ =
=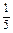 ,
,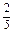 ,
,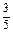 ,
,∴P(
 <
< <
< )=P(
)=P( =
=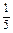 )+P(
)+P( =
=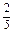 )+P(
)+P( =
=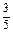 )
)=
 +
+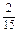 +
+ =
=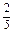 .
.
练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目

 ,其中
,其中 的各位数中,
的各位数中, ,
,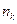 (
( 2,3,4,5)出现0的概率为
2,3,4,5)出现0的概率为 ,出现1的概率为
,出现1的概率为 ,记
,记 ,当该计算机程序运行一次时,求随机变量
,当该计算机程序运行一次时,求随机变量 的分布列和数学期望。
的分布列和数学期望。 ,求
,求 服从二项分布,
服从二项分布,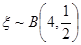 ,则
,则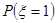 的值为
的值为 
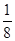


 元。
元。 ,
, .
. 的值;
的值; ,求
,求 .
. 的分布列如下,则
的分布列如下,则 的值是( ).
的值是( ).





