题目内容
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表，即杨辉三角，这是数学史上的一个伟大成就.在“杨辉三角”中，若去除所有为1的项，依次构成数列2，3，3，4，6，4，5，10，10，5，…，则此数列的前56项和为（ ）
A.2060B.2038C.4084D.4108
【答案】C
【解析】
先由题意，根据杨辉三角的特征，得到杨辉三角形的前
行的和，再求出去除所有为
的项之和，构成数列的和，进而可求出结果.
次二项式系数对应杨辉三角形的第
行，例如
，系数分别为，
，，对应杨辉三角形的第
行，
令
，就可以求出该行的系数之和；第行为
，第行为
，第行为
，以此类推，即每一行数字之和构成首项是，公比是的等比数列，
则杨辉三角形的前行的和为
，
若去除所有为的项，则剩下的每一行的个数为，，，...，可看成以为首项，以为公差的等差数列，则
，
当
时，
，去除两端的可得
，
则此数列的前
项的和为：
.
故选：C.
王后雄学案教材完全解读系列答案
海淀课时新作业金榜卷系列答案
期末金牌卷系列答案【题目】某品牌经销商在一广场随机采访男性和女性用户各50名，其中每天玩微信超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如下：
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
（1）根据以上数据，能否有95%的把握认为“微信控”与“性别”有关？
（2）现从调查的女性用户中按分层抽样的方法选出5人，求所抽取的5人中“微信控”和“非微信控”的人数；
（3）从（2）中抽取的5位女性中，再随机抽取3人赠送礼品，试求抽取3人中恰有2人位“微信控”的概率.
参考公式: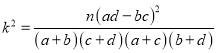 
，其中
.
参考数据：
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
【题目】有甲、乙两个班级进行数学考试，按照大于等于85分为优秀，85分以下为非优秀统计成绩，得到如下所示的列联表：
优秀 | 非优秀 | 总计 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
总计105 |
已知在全部105人中随机抽取1人，成绩优秀的概率为
，则下列说法正确的是（ ）
参考公式：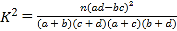
附表：
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30，b的值为35
B.列联表中c的值为15，b的值为50
C.根据列联表中的数据，若按95%的可靠性要求，能认为“成绩与班级有关系”
D.根据列联表中的数据，若按95%的可靠性要求，不能认为“成绩与班级有关系”
