题目内容
【题目】已知函数![]() (
(![]() 为自然对数的底数),
为自然对数的底数),![]() 是
是![]() 的导函数.
的导函数.
(Ⅰ)当![]() 时,求证
时,求证![]() ;
;
(Ⅱ)是否存在正整数![]() ,使得
,使得![]() 对一切
对一切![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最大值;若不存在,说明理由.
的最大值;若不存在,说明理由.
【答案】(1)详见解析;(2)存在且为![]() .
.
【解析】
(Ⅰ)要证明函数不等式![]() (
(![]() ),注意到
),注意到![]() ,因此我们可先研究函数的性质特别是单调性,这可通过导数的性质确定;
,因此我们可先研究函数的性质特别是单调性,这可通过导数的性质确定;
(Ⅱ)首先把不等式具体化,即不等式![]() 为
为![]() ,注意到特殊情形,
,注意到特殊情形,![]() 时,不等式为
时,不等式为![]() ,因此
,因此![]() 的值只有为1或2,因此只要证
的值只有为1或2,因此只要证![]() 时,不等式
时,不等式![]() 恒成立即可,这仍然通过导数研究函数的单调性证得结论,为了确定导数的正负的方便性,把不等式变为
恒成立即可,这仍然通过导数研究函数的单调性证得结论,为了确定导数的正负的方便性,把不等式变为![]() ,因此只要研究函数
,因此只要研究函数![]() 的单调性,求得最小值即可.
的单调性,求得最小值即可.
试题解析:(Ⅰ)当![]() 时,
时,![]() ,则
,则![]() ,
,
令![]() ,则
,则![]() ,
,
令![]() ,得
,得![]() ,故
,故![]() 在
在![]() 时取得最小值,
时取得最小值,
![]() 在
在![]() 上为增函数,
上为增函数,
![]() ,
,
(Ⅱ)![]() ,
,
由![]() ,得
,得![]() 对一切
对一切![]() 恒成立,
恒成立,
当![]() 时,可得
时,可得![]() ,所以若存在,则正整数
,所以若存在,则正整数![]() 的值只能取1,2.
的值只能取1,2.
下面证明当![]() 时,不等式恒成立,
时,不等式恒成立,
设![]() ,则
,则![]() ,
,
由(Ⅰ)![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
![]() ,
,
![]() 当
当![]() 时,不等式恒成立
时,不等式恒成立
所以![]() 的最大值是2.
的最大值是2.

练习册系列答案
相关题目
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 | b | |
乙班 | c | 30 | |
总计105 |
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
参考公式: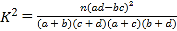
附表:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
A.列联表中c的值为30,b的值为35
B.列联表中c的值为15,b的值为50
C.根据列联表中的数据,若按95%的可靠性要求,能认为“成绩与班级有关系”
D.根据列联表中的数据,若按95%的可靠性要求,不能认为“成绩与班级有关系”