题目内容
【题目】已知正项数列{an}的前n项和为Sn , 且 ![]() =
= ![]() ,a1=m,现有如下说法: ①a2=5;
,a1=m,现有如下说法: ①a2=5;
②当n为奇数时,an=3n+m﹣3;
③a2+a4+…+a2n=3n2+2n.
则上述说法正确的个数为( )
A.0个
B.1个
C.2个
D.3个
【答案】D
【解析】解: ![]() =
= ![]() ,a1=m,
,a1=m,
∴(an+1+1)(an+1)=6(Sn+n),①n=1时,(a2+1)×(m+1)=6(m+1),∵m+1>0时,∴a2=5.②n≥2时,(an+1)(an﹣1+1)=6(Sn﹣1+n﹣1),
∴(an+1)(an+1﹣an﹣1)=6an+6,an>0,
∴an+1﹣an﹣1=6.
∴当n=2k﹣1(k∈N*)为奇数时,数列{a2k﹣1}为等差数列,∴an=a2k﹣1=m+(k﹣1)×6=3n+m﹣3.③当n=2k(k∈N*)为偶数时,数列{a2k}为等差数列,∴an=a2k=5+(k﹣1)×6=3n﹣1.
∴a2+a4+…+a2n=6×(1+2+…+n)﹣n= ![]() ﹣n=3n2+2n.
﹣n=3n2+2n.
因此①②③都正确.
故选:D.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系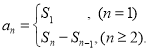 ).
).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目



