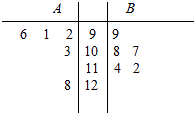��Ŀ����
����Ŀ��ijˮ���깺��ij��ˮ���ijɱ�Ϊ20Ԫ/kg�������г����з��֣�����ˮ����δ��30������۵���P��Ԫ/kg����ʱ��t���죩֮��ĺ�����ϵʽΪ ![]() ��������Q��kg����ʱ��t���죩�ĺ�����ϵʽΪQ=��2t+120��
��������Q��kg����ʱ��t���죩�ĺ�����ϵʽΪQ=��2t+120��
����ˮ������һ����������������������Ƕ��٣�
����Ϊ��Ӧ����������ƶ�����٣��õ����ÿ����1kgˮ���;���n��n��N��Ԫ��������ƶ��������ʹ����������������ʱ��t��t��N��������������������n��ֵ��
���𰸡��⣺����������Ϊy��Ԫ������ 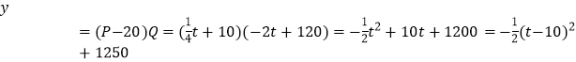 ��
��
��t=10ʱ��ymax=1250��
����ʮ���������������������Ϊ1250Ԫ��
����������������ΪW��Ԫ��
�� ![]() =
= ![]() ��
��
��W=f��t��������κ���f��t����ͼ�����£��Գ���t=2n+10��
��������ʱ��t��t��N��������������Ҿ�������
�� 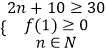 �����n=10
�����n=10
����������������֪�����ɵõ�����y�ĺ�������ʽ�������ö��κ����䷽�ó���t=10ʱ��ymax=1250������������ɵ� W�ĺ�������ʽ���Ѹú�����Ϊ����t�Ķ��κ������ɶ��κ���ͼ������ʿɵó�![]() ,�������������ó�
,�������������ó�![]() ,�����õ�n��ֵ��
,�����õ�n��ֵ��

��ϰ��ϵ�д�
 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�
�����Ŀ