题目内容
【题目】已知首项为1的正项数列{an}满足an+12+an2＜ 
，n∈N* ， Sn为数列{an}的前n项和．
（1）若a2= 
，a3=x，a4=4，求x的取值范围；
（2）设数列{an}是公比为q的等比数列，若 
＜Sn+1＜2Sn ， n∈N* ， 求q的取值范围；
（3）若a1 ， a2 ， …，ak（k≥3）成等差数列，且a1+a2+…+ak=120，求正整数k的最小值，以及k取最小值时相应数列a1 ， a2 ， …，ak ．
【答案】
（1）解：∵首项为1的正项数列{an}满足an+12+an2＜ 
，n∈N*，化为（2an+1﹣an）（an+1﹣2an）＜0，
∴ 
＜2．
又a2= 
，a3=x，a4=4，
∴ 
， 
，
解得：2＜x＜3．
∴x的取值范围是（2，3）
（2）解：由于首项为1的正项数列{an}，
∵ ＜2．∴ 
．
①q=1时，n=1时不满足： 
＜Sn+1＜2Sn，n∈N*，因此q≠1．
②可得 
＜2 
，
＜q＜1时，化为2qn+1﹣qn＜1，qn+1﹣2qn+1＞0，由于qn（2q﹣1）＜1，因此2qn+1﹣qn＜1恒成立；由qn＜q，可得q2n＜qn+1，∴qn 
，∴2qn 
＜1+qn+1，因此qn+1﹣2qn+1＞0恒成立，可得： ＜q＜1．
2＞q＞1时，化为2qn+1﹣qn﹣1＞0，qn+1﹣2qn+1＜0，无解，舍去．
综上可得： ＜q＜1
（3）解：设首项为1的正项数列{an}的公差为d，d≥0，
由 ＜2，可得 ＜ 
＜2，
化为1+（n﹣1）d＜2（1+nd）＜4[1+（n﹣1）d]，
n=1时，0≤d＜1；n=2时，d≥0；
n≥3时，d≥0．
综上可得：0≤d＜1．
∵a1，a2，…，ak（k≥3）成等差数列，a1+a2+…+ak=120，
∴k+ 
d=120，
k=1时，不成立，舍去．
k≥2时，解得d= 
，
∵0≤d＜1．
∴0≤ ＜1．
解得：15＜k≤120．
∴满足条件的正整数k的最小值为16，此时d= 
，
相应数列的通项公式为：an=1+ （n﹣1）= 
．
数列为：1， 
【解析】（1）首项为1的正项数列{an}满足an+12+an2＜ ，n∈N* ， 化为（2an+1﹣an）（an+1﹣2an）＜0，解得： ＜2．又a2= ，a3=x，a4=4，代入解出即可得出．（2）由于首项为1的正项数列{an}，由于 ＜2．可得 ．对q分类讨论：q=1时，n=1时不满足条件，因此q≠1．②由 ＜2 ， ＜q＜1时，经过验证成立： ＜q＜1.2＞q＞1时，化为2qn+1﹣qn﹣1＞0，qn+1﹣2qn+1＜0不成立，舍去．（3）设首项为1的正项数列{an}的公差为d，d≥0，由 ＜2，化为1+（n﹣1）d＜2（1+nd）＜4[1+（n﹣1）d]．分类讨论：n=1时，n=2时，n≥3时，可得：0≤d＜1．根据a1 ， a2 ， …，ak（k≥3）成等差数列，a1+a2+…+ak=120，可得k+ d=120，k=1时，不成立，舍去．k≥2时，解得d= ，代入解得：15＜k≤120．即可得出．
【考点精析】通过灵活运用等比数列的通项公式（及其变式）和数列的前n项和，掌握通项公式：
；数列{an}的前n项和sn与通项an的关系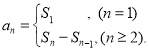
即可以解答此题．
