题目内容
【题目】已知抛物线C:y2=2px(p>0)的焦点F与双曲线![]() 的一个焦点重合,过焦点F的直线l交抛物线于A,B两点.
的一个焦点重合,过焦点F的直线l交抛物线于A,B两点.
(1)求抛物线C的方程;
(2)记抛物线C的准线与x轴的交点为N,试问是否存在常数λ∈R,使得![]() 且
且![]() 都成立?若存在,求出实数λ的值;若不存在,请说明理由.
都成立?若存在,求出实数λ的值;若不存在,请说明理由.
【答案】(1)y2=4x(2)存在,λ=2或![]()
【解析】
(1)由双曲线方程求出焦点坐标,结合题意可得p=2,即得抛物线方程;
(2)依题意设![]() ,联立
,联立![]() ,消去
,消去![]() ,得
,得![]() .利用根与系数的关系结合
.利用根与系数的关系结合![]() ,求得
,求得![]() ,再由
,再由![]() 求得
求得![]() 的值,即可求得实数λ的值.
的值,即可求得实数λ的值.
(1)由双曲线![]() ,得
,得![]() ,
,![]() ,
,
则![]() ,即双曲线的焦点坐标为(﹣1,0),(1,0),
,即双曲线的焦点坐标为(﹣1,0),(1,0),
由抛物线C:y2=2px(p>0),且其焦点与双曲线![]() 的一个焦点重合,
的一个焦点重合,
可得![]() ,p=2.
,p=2.
∴抛物线方程为y2=4x;
(2)依题意,F(1,0),设l:x=ty+1,A(x1,y1),B(x2,y2),
联立![]() ,消去x,得y2﹣4ty﹣4=0.
,消去x,得y2﹣4ty﹣4=0.
∴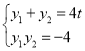 ,…①
,…①
且x1=ty1+1,x2=ty2+1,
又![]() ,则(1﹣x1,﹣y1)=λ(x2﹣1,y2),即y1=﹣λy2,
,则(1﹣x1,﹣y1)=λ(x2﹣1,y2),即y1=﹣λy2,
代入①得,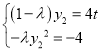 ,消去y2得,
,消去y2得,![]() ,且N(﹣1,0),
,且N(﹣1,0),
|NA|2+|NB|2=(x1+1)2+y12+(x2+1)2+y22=x12+x22+2(x1+x2)+2+y12+y22
![]() 2
2![]()
![]() 4t(y1+y2)+8,
4t(y1+y2)+8,
=(t2+1)(16t2+8)+4t4t+8=16t4+40t2+16.
由16t4+40t2+16![]() ,解得
,解得![]() 或
或![]() (舍),
(舍),
∴![]() ,故λ=2或
,故λ=2或![]() .
.

【题目】研究机构对某校学生往返校时间的统计资料表明:该校学生居住地到学校的距离![]() (单位:千米)和学生花费在上学路上的时间
(单位:千米)和学生花费在上学路上的时间![]() (单位:分钟)有如下的统计资料:
(单位:分钟)有如下的统计资料:
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明![]() 与
与![]() 有线性相关关系,试求:
有线性相关关系,试求:
(1)判断![]() 与
与![]() 是否有很强的线性相关性?
是否有很强的线性相关性?
(相关系数![]() 的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
(2)求线性回归方程![]() (精确到0.01);
(精确到0.01);
(3)将![]() 分钟的时间数据
分钟的时间数据![]() 称为美丽数据,现从这6个时间数据
称为美丽数据,现从这6个时间数据![]() 中任取2个,求抽取的2个数据全部为美丽数据的概率.
中任取2个,求抽取的2个数据全部为美丽数据的概率.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
参考公式: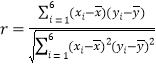 ,
,