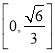题目内容
【题目】在由数字1，2，3，4，5组成的所有没有重复数字的四位数中，大于3145且小于4231的数共有（ ）
A.27个B.28个C.29个D.30个
【答案】A
【解析】
根据题意，按四位数的千位数字不同分2种情况讨论：求出每种情况下四位数的个数，由加法原理计算可得答案．
】解：根据题意，分2种情况，
四位数的千位数字为3，
其百位数字为1时，有3154符合条件，
其百位数字可以为2、4、5时，有3种情况，
在剩下的3个数字中任选2个，安排在十位、个位，有
种情况，
此时有
个符合条件的四位数；
四位数的千位数字为4，
其百位数字为1时，在剩下的3个数字中任选2个，安排在十位、个位，有种情况，
其百位数字为2时，只有4213、4215符合条件，
此时有
个符合条件的四位数；
则有
个符合条件的四位数；
故选：A．
练习册系列答案
相关题目
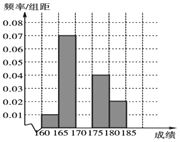
【题目】某高校在2016年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如表所示．
组号 | 分组 | 频数 | 频率 |
第1组 |
| 5 |
|
第2组 |
| n |
|
第3组 |
| 30 | p |
第4组 |
| 20 |
|
第5组 |
| 10 |
|
合计 | 100 |
|
（1）求频率分布表中n，p的值，完善频率分布直方图并估计该组数据的中位数
保留l位小数
；
（2）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取6名学生进入第二轮面试，学校决定从这6名学生中随机抽取2名学生接受甲考官的面试，求第4组至少有1名学生被甲考官面试的概率．
