题目内容
【题目】研究机构对某校学生往返校时间的统计资料表明:该校学生居住地到学校的距离![]() (单位:千米)和学生花费在上学路上的时间
(单位:千米)和学生花费在上学路上的时间![]() (单位:分钟)有如下的统计资料:
(单位:分钟)有如下的统计资料:
到学校的距离 | 1.8 | 2.6 | 3.1 | 4.3 | 5.5 | 6.1 |
花费的时间 | 17.8 | 19.6 | 27.5 | 31.3 | 36.0 | 43.2 |
如果统计资料表明![]() 与
与![]() 有线性相关关系,试求:
有线性相关关系,试求:
(1)判断![]() 与
与![]() 是否有很强的线性相关性?
是否有很强的线性相关性?
(相关系数![]() 的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
的绝对值大于0.75时,认为两个变量有很强的线性相关性,精确到0.01)
(2)求线性回归方程![]() (精确到0.01);
(精确到0.01);
(3)将![]() 分钟的时间数据
分钟的时间数据![]() 称为美丽数据,现从这6个时间数据
称为美丽数据,现从这6个时间数据![]() 中任取2个,求抽取的2个数据全部为美丽数据的概率.
中任取2个,求抽取的2个数据全部为美丽数据的概率.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]()
参考公式: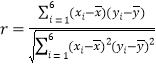 ,
,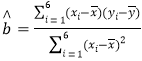
【答案】(1)![]() 与
与![]() 有很强的线性相关性;(2)
有很强的线性相关性;(2)![]() ;(3)
;(3)![]()
【解析】
(1)通过计算线性相关系数可得答案;(2)根据题意写出统计表,用统计表中的数据求出横标和纵标的平均数,利用最小二乘法做出线性回归方程的系数![]() 、
、![]() ,写出线性回归方程;(3)根据(2)中求出的线性回归方程,求出符合要求的数据个数,再列出全部情况,由古典概型的公式,求出所求概率.
,写出线性回归方程;(3)根据(2)中求出的线性回归方程,求出符合要求的数据个数,再列出全部情况,由古典概型的公式,求出所求概率.
(1) ∴
∴![]() 与
与![]() 有很强的线性相关性
有很强的线性相关性
(2)依题意得![]()
![]() ,
,![]() ,
,![]()
所以
又因为![]()
故线性回归方程为![]()
(3)由(2)可知,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,所以满足
,所以满足![]() 分钟的美丽数据共有3个,设3个美丽数据为
分钟的美丽数据共有3个,设3个美丽数据为![]() 、
、![]() 、
、![]() ,另3个不是美丽数据为
,另3个不是美丽数据为![]() 、
、![]() 、
、![]() ,则从6个数据中任取2个共有15种情况,即
,则从6个数据中任取2个共有15种情况,即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,其中,抽取到的数据全部为美丽数据的有3种情况,即
,其中,抽取到的数据全部为美丽数据的有3种情况,即![]() ,
,![]() ,
,![]() .所以从这6个数据
.所以从这6个数据![]() 中任取2个,抽取的2个数据全部为美丽数据的概率为
中任取2个,抽取的2个数据全部为美丽数据的概率为![]()

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目