题目内容
【题目】如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1 . 求证: 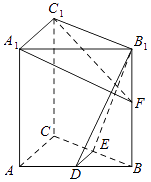
(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
【答案】
(1)证明:∵D,E为中点,
∴DE为△ABC的中位线,∴DE∥AC,
又∵ABC﹣A1B1C1为棱柱,
∴AC∥A1C1,∴DE∥A1C1,
又∵A1C1平面A1C1F,且DEA1C1F,
∴DE∥平面A1C1F
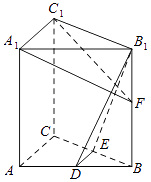
(2)证明:∵ABC﹣A1B1C1为直棱柱,
∴AA1⊥平面A1B1C1,∴AA1⊥A1C1,
又∵A1C1⊥A1B1且AA1∩A1B1=A1,AA1,A1B1平面AA1B1B,
∴A1C1⊥平面AA1B1B,
又A1C1∥AC∥DE,∴DE⊥平面AA1B1B,
又∵A1F平面AA1B1B,∴DE⊥A1F
又∵A1F⊥B1D,DE∩B1D=D,且DE,B1D平面B1DE,
∴A1F⊥平面B1DE,
又∵A1FA1C1F,∴平面B1DE⊥平面A1C1F
【解析】(1)推导出DE∥AC,从而DE∥A1C1 , 由此能证明DE∥平面A1C1F.(2)推导出AA1⊥A1C1 , 从而A1C1⊥平面AA1B1B,进而DE⊥平面AA1B1B,再由DE⊥A1F,得A1F⊥平面B1DE,由此能证明平面B1DE⊥平面A1C1F.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目