题目内容
【题目】求分别满足下列条件的直线l的方程:
(1)斜率是 ![]() ,且与两坐标轴围成的三角形的面积是6;
,且与两坐标轴围成的三角形的面积是6;
(2)经过两点A(1,0)、B(m,1);
(3)经过点(4,-3),且在两坐标轴上的截距的绝对值相等.
【答案】
(1)解:设直线l的方程为y= ![]() x+b.
x+b.
令y=0,得x=- ![]() b,
b,
∴ ![]() |b·(-
|b·(- ![]() b)|=6,b=±3.
b)|=6,b=±3.
∴直线l的方程为y= ![]() x±3.
x±3.
(2)解:当m≠1时,直线l的方程是
![]() ,即y=
,即y= ![]() (x-1)
(x-1)
当m=1时,直线l的方程是x=1.
(3)解:设l在x轴、y轴上的截距分别为a、b.
当a≠0,b≠0时,l的方程为 ![]() =1;
=1;
∵直线过P(4,-3),∴ ![]()
又∵|a|=|b|,
∴ 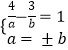 ,解得
,解得 ![]() ,或
,或 ![]() .
.
当a=b=0时,直线过原点且过(4,-3),
∴l的方程为y=- ![]() x.
x.
综上所述,直线l的方程为x+y=1或 ![]() =1或y=-
=1或y=- ![]() x.
x.
【解析】(1)先设出直线l的斜截式,再用含b的式子表示出直线l与两坐标轴的截距,再利用与两坐标轴围成的三角形的面积是6即可求得b的值,从而求得直线l的方程;(2)再利用两点式求直线的方程时需考虑是否直线与坐标轴平行,若平行则不能使用两点式;(3)先讨论截距不为0时的情况,设出直线l的截距式方程,再利用两坐标轴的截距绝对值相等即可求得直线l的方程;再讨论截距为0时的情况.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目